摘要: 針對某大型龍門加工中心的橫梁進行多參數輕量化設計。對橫梁結構進行有限元分析得出其初始的受力及變形情況。在保證橫梁結構不變的情況下,以橫梁的最大變形為約束條件,選擇橫梁的筋板厚度、出砂孔孔徑等7 個結構參數作為設計變量,運用實驗設計法對橫梁進行輕量化設計。得到在橫梁結構不變的條件下,7參數聯合優化設計的設計變量參考值以及橫梁總質量的響應變化值,優化設計的最優結果為橫梁變形增加1. 81%的同時質量減輕2. 97%。
0 引言
橫梁是數控機床的主要支撐部件,傳統數控機床的橫梁設計采用類比的經驗設計方法,而且在驗算橫梁結構的強度與剛度時,常選擇過大的安全系數,造成所設計橫梁的結構尺寸與重量偏大,所以需要采用輕量化設計方法對其進行優化設計。
優化設計作為機械設計中一種重要的科學設計方法,使得在解決復雜設計問題時,能從眾多的設計方案中尋找到盡可能完美的或最適宜的設計方案 。輕量化設計是優化設計的一種,目的是通過對構件進行設計,使構件在滿足使用要求的情況下重量盡可能地輕 。趙韓等人 利用參數化有限元法對液壓機機身進行了輕量化設計; 呂國坤等人 基于遺傳算法和響應面法對驅動橋橋殼進行了輕量化設計; 譚志洪等人 在天花板結構優化設計中采用了多方案優化設計,使得天花板鋼耗降幅高達30% ; 王樹英等人 對燃料電池轎車的前副車車架進行了輕量化設計,以模態特性為約束條件,使得車架自身質量得到大幅度降低; 萬長東 對汽車發動機罩殼進行了多工況下的結構優化分析,使得汽車發動機在罩殼性能提升的同時,結構質量得到減輕。可見,通過輕量化設計方法,不僅可以減輕結構質量,而且可以解決傳統方法所不能解決的比較復雜的優化設計問題。
鑒于此,筆者希望通過輕量化設計方法對橫梁結構進行多參數輕量化協同設計。首先,采用有限元分析技術獲得橫梁結構的應力場和變形場分布情況; 然后,根據優化要求建立優化模型,確定優化目標、設計變量、狀態變量和約束函數,結合優化算法獲得計算結果; 最后,在確保橫梁結構滿足使用強度的基礎上,達到減少材料用量的目的。
橫梁結構輕量化方法的實施流程如圖1 所示。首先,對一個新工程或新產品的功能進行分析,明確其具體要求、工作環境及外界條件,從而提出相應的解決方案; 其次,根據工程要求,簡化實際模型,將對輕量化目標影響較大的參數確定為設計變量,利用CAD軟件建立橫梁的參數化模型; 再次,將各方案所得參數化模型導入Ansys 軟件的Design Modeler 模塊( 用于實現Ansys 和外部CAD 的交互) ,分別進行仿真計算,通過Simulations 模塊得出橫梁的應力、應變等云圖,并初步比較這些方案的分析結果; 然后利用Ansys軟件中的Design Xplorer 模塊對各方案進行優化分析,通過實驗設計( DOE) 法實現方案優化設計; 最后,綜合考慮生產、工藝、運輸和安裝等多方面因素,在多個方案中進行優化比較且在多個目標之間相互協調,從中找出最佳方案,確定橫梁的最優結構形式。
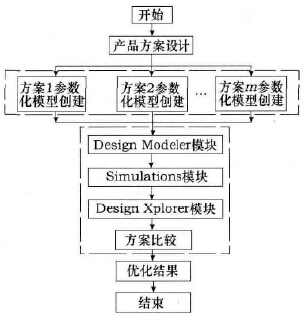
圖1 橫梁結構輕量化方法的實施流程
1、 原橫梁結構分析
本文是在參考文獻[9]的基礎上對橫梁進行的多參數輕量化分析,所以此處的原橫梁結構分析直接引用參考文獻 的分析結果。筆者在參考文獻 中針對某大型龍門加工中心的橫梁在實際工況下的應力及變形進行了分析,橫梁三維裝配體模型簡圖如圖2 所示,橫梁的質量為14 729kg。根據參考文獻[9]的分析結果可知: 當滑鞍在橫梁中間位置、滑枕伸出長度為全長的60%、機床主軸最大切削扭矩為5 010N·m時,橫梁的變形量最大,將此工況下的橫梁模型作為優化分析的基礎模型,原橫梁模型的變形仿真結果、原橫梁裝配體模型的應力仿真結果分別如圖3 和圖4 所示。
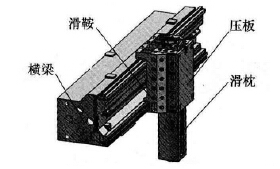
圖2 橫梁三維裝配體模型簡圖
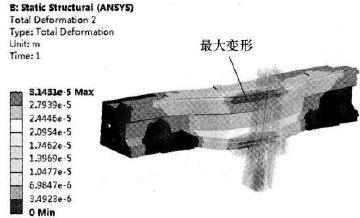
圖3 原橫梁模型的變形仿真結果
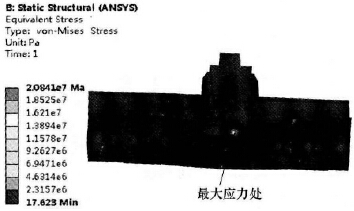
圖4 原橫梁裝配體模型的應力仿真結果

2 、橫梁輕量化設計模型建立
在進行橫梁結構的優化分析過程中,結構輕量化是主要目標,主要約束條件為橫梁的變形,在滿足給定的剛度、強度的約束條件下使橫梁的質量達到最小。
2. 1 目標函數
通過優化結構的體積來達到減輕結構質量的目的,以質量最輕作為目標函數,即:

2. 2 設計變量
根據設計要求,考慮到橫梁結構組成較復雜、尺寸變量較多,太多的設計變量增大了收斂到局部最小而非全局最小的概率,所以應盡量減少設計變量數量。采用變量關聯的方法,以橫梁結構上相互關聯的尺寸建立傳遞方程式,即設計變量x 為:

通過分析橫梁結構可知,橫梁主要由外部殼體和內部筋板組成,由于橫梁外部殼體的結構與尺寸不可變動,故選取橫梁內部筋板厚度,上、下出砂孔孔徑等7 個參數即n = 7,進行多參數聯合優化。7 個優化參數示意如圖5 所示,對7 個優化參數的取值情況描述如下。
1) 交叉筋板厚度t1( 見圖5a) ,t1的優化初始值為25mm,其優化取值范圍為22. 5 ~ 27. 5mm。
2) 豎直筋板厚度t2( 見圖5b) ,t2的優化初始值為20mm,其優化取值范圍為18 ~ 22mm。
3) 內部交叉筋板上的出沙孔孔徑t3,t3的優化初始值為200mm,其優化取值范圍為180 ~ 220mm。
4) 橫梁后部的上出沙孔孔徑t4( 見圖5c) ,t4的優化初始值為200mm,其優化取值范圍為180 ~ 220mm。
5) 橫梁后部的下出沙孔孔徑t5( 見圖5c) ,t5的優化初始值為200mm,其優化取值范圍為180 ~ 220mm。
6) 橫梁側面出沙孔孔徑t6( 見圖5c) ,t6的優化初始值為180mm,其優化取值范圍為162 ~ 198mm。
7) 橫梁底部出沙孔孔徑t7( 見圖5c) ,t7的優化初始值為200mm,其優化取值范圍為180 ~ 220mm。
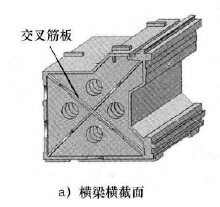
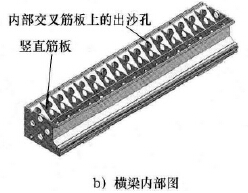
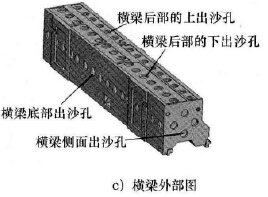
圖5 7 個優化參數示意


最終得到的橫梁結構優化設計的數學模型為:
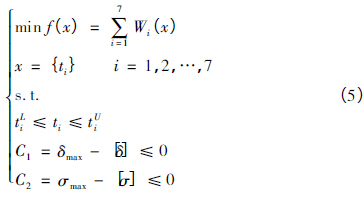
式中: tUi、tLi分別為ti的上限和下限。運用Ansys 軟件提供的基于實驗設計( DOE) 方法[9],根據輸入參數的數目,利用目標驅動優化( GoalDrive Optimization,GDO) 技術,采集設計參數樣點,計算每個樣點的響應結果,利用二次插值函數構造設計空間的響應面或設計曲線,最終獲得優化的解集。本文提出的橫梁輕量化設計,就是在優化求解的實施過程中保持橫梁結構不變,進行基于DOE 技術的多參數協同優化,獲得橫梁輕量化設計的最優結果。
2. 4 橫梁輕量化分析結果
根據本文建立的橫梁輕量化設計模型,設置約束條件( 優化后變形增加量不超過5%,最大應力不超過最大應力限值) 并輸出結果,通過軟件仿真可計算出3組優化結果以供選擇,如表1 所示,其中第1 組實驗各構件的尺寸參數取值分別為: t1 = 22. 642mm,t2 =19. 073mm,t3 = 195. 56mm,t4 = 196. 74mm,t5 = 213. 79mm,t6 = 190. 74mm,t7 = 197. 24mm,此時的橫梁最大變形量為3. 2 × 10 - 5m,比優化前增加了1.81%,橫梁質量為14 291kg,比優化前減少了2. 97%,質量減輕效果相對最優。為了觀察各個設計變量對分析結果的影響程度,利用Ansys 軟件后處理模塊進行靈敏度分析,得到各構件尺寸參數對輸出結果的影響程度如圖6 所示,從圖6 所示可以看出,橫梁內部交叉筋板厚度t1與豎直筋板厚度t2對橫梁變形及橫梁質量的影響程度遠大于其他5 個因素,其他5 個因素對于橫梁變形的影響程度由大到小依次為: t6 > t4 > t5 > t7 > t3; 對于質量的影響程度由大到小依次為: t6 > t4 > t3 > t5 >t7,因此,在下一步的橫梁結構設計研究中可著重考慮t1和t2兩個影響因素。優化后橫梁變形及質量的變化情況如表2 所示。
表1 優化結果

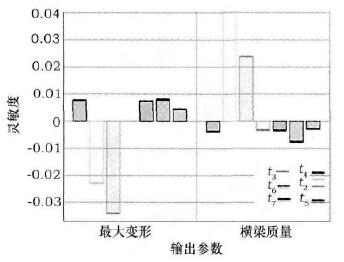
圖6 構件尺寸參數對輸出結果的影響程度
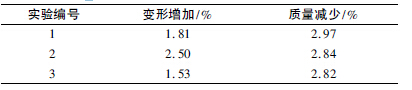
表2 優化后橫梁變形及質量的變化情況
3 、結語
本文對某大型龍門加工中心橫梁進行了包含橫梁的筋板厚度、出砂孔孔徑等7 個構件尺寸參數在內的多參數輕量化設計,得到在橫梁基本結構不變的前提下,橫梁變形增加1. 81%的同時質量減少2. 97%的優化結果。
今后將重點研究橫梁所有組成構件的結構尺寸參數對輸出結果的影響,并找出影響最顯著的參數,為進一步的橫梁結構優化乃至變結構輕量化設計提供有益的參考。
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com





