數控機床三維空間幾何誤差補償方法
2018-6-5 來源:南京航空航天大學 機電學院 作者:朱建偉,陳蔚芳,鄭德星,朱赤洲
摘要: 為了提高數控機床的加工精度,在系統分析數控機床幾何誤差常用補償方法基礎上,提出了基于數控系統插補數據的幾何誤差補償方法,并將誤差補償功能集成于國產數控系統中,以提高國產數控系統的綜合性能。通過實驗與仿真結果表明,數控系統插補數據的幾何誤差補償方案能顯著提高數控機床的加工精度。
關鍵詞: 數控機床; 數控系統; 誤差補償; 機床精度
0、 引言
隨著機械制造業的不斷發展,精密加工已逐漸成為現代制造業的主要趨勢,誤差補償技術也因此獲得了迅速發展。誤差補償有硬件補償和軟件補償2種補償策略。硬件補償專用性比較強,在國內外都沒有得到較好的發展;而軟件補償則通用性較強,國內外有很多學者對其進行了研究。Y.Y. Hsu 和 S.S. Wang 等人提出了一種新的五軸機床誤差補償解耦方法,分別計算出機床轉動軸和移動軸的誤差,并應用于機床后置處理中,獲得了優化的NC程序; Ibaraki 等提出多軸機床幾何誤差測量新方法,并完成誤差補償; Feng Huo 等人在系統的研究了影響輪廓銑削加工精度影響因素的基礎上,分析了各因素的補償方法,并實驗驗證了補償方法的可行性; 在國內,何振亞在研究 PMAC 卡的運動誤差補償功能中,用 Matlab 實現了對機床空間誤差的可視化分析及補償。王維等人提出了一種包含幾何誤差與熱誤差的綜合誤差建模方法,采用數控系統的坐標偏置命令,進行實時在線補償,取得了較好的效果; 韓飛飛等人利用機床幾何誤差分析法,通過激光干涉儀檢測機床各項誤差,發現了各個運動軸及某一軸的不同工作區間誤差規律,由此提升機床加工精度。
目前國內大多數數控機床空間誤差補償方法都很難與數控系統真正集成,僅是簡單地將誤差映射給加工過程,補償效果不夠理想。因此,有必要將空間誤差補償功能嵌入到數控系統中,實現與數控系統的集成,提高其實用性、實時性和可靠性。
文中系統研究了數控機床三維空間誤差補償方法,著重研究了不同補償方法的工作原理,提出了基于數控系統插補數據的誤差補償方法,有效提高了數控機床精度。
1、 數控機床三維幾何誤差補償方法
常見的數控機床三維空間誤差補償方法主要有以下幾種。
1) NC 代碼修正補償法
在數控機床誤差的影響下,如果按照理想的 NC 代碼對零件進行加工則存在加工誤差,為了消除數控機床誤差對加工過程的影響,可以對 NC 代碼進行修正,用修正后的數控加工程序對工件進行加工,從而實現數控機床誤差的補償。補償流程圖如圖 1 所示,將 NC 代碼輸入到誤差補償軟件中,然后生成理想刀具路徑,并根據誤差補償預測模型對理想刀具路徑進行修正,得到實際的刀具路徑軌跡,最后生成修正后的 NC 代碼。該方法對數控機床幾何誤差的補償具有良好的效果。
2) 接口式 NC 型誤差補償法
接口式 NC 型誤差補償方法是將由誤差預測模型計算得到的誤差值,疊加到數控系統的插補過程。基本工作原理如下: 通過特定的誤差補償接口,NC 系統將當前機床的各項參數( 機床位置參數和刀具信息等) 傳遞給誤差預測模型,經過誤差預測模型計算出相應的誤差值反饋給NC 系統,NC 系統對誤差值進行處理,生成新的數控程序,實現誤差的補償。如圖 2 所示。
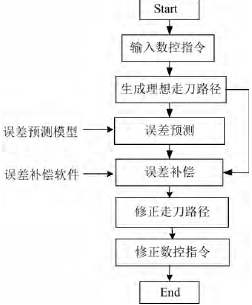
圖 1 數控加工指令修正補償示意圖
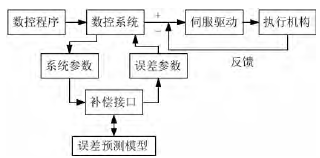
圖 2 接口式 NC 型誤差補償示意圖
2、 基于數控系統插補數據的誤差補償方法
在接口式 NC 型誤差補償方法的基礎上,提出了一種基于數控系統插補數據的數控機床三維空間誤差補償方法。這種補償方法是基于數控系統的動態補償,它將數控機床三維空間誤差融合到數控系統中,通過外部開發補償軟件修正數控系統中的粗插補數據達到對數控機床三維空間誤差的補償目的。補償流程如圖 3 所示。
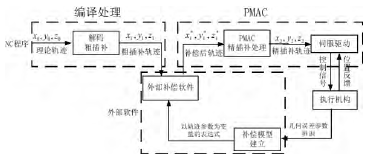
圖 3 基于數控系統插補數據的補償方法
外部補償軟件可以補償幾何誤差和熱誤差。數控機床的幾何誤差是一種準靜態的誤差源,具有一定的靜態特性,在某一環境溫度范圍內可視為常量,較為容易與數控系統集成實現其誤差的實時補償; 而對于高精度的數控機床,熱誤差是最大誤差源,占機床總誤差的 40%以上。熱誤差模型的建立和機床的結構是密切相關的,通常采用在機床的關鍵點布置溫度測量傳感器,采集得到相應的敏感點溫度,最后通過相應的誤差模型計算出誤差值,對加工過程進行實時的補償。
外部補償軟件獲取和修正數控系統數據流的前提是數控系統應提供一個數據接口實現與外部軟件的信息交互,因此需要進行數據接口的編寫。此外,在實現誤差補償功能時外部補償軟件和數控系統應同時運行,操作起來比較復雜,工作效率相對較低。考慮到這些因素后,作如下改進處理,即將外部補償軟件作為一個模塊嵌入到數控系統當中,以此提高數控系統的智能化和集成化程度。
上述補償方法是 NC 型誤差補償法的一種特殊類型。該方法相對于 NC 代碼修正補償來說有很大的優點,機床的參數可以直接在數控系統的數據流中提取,并且經過進一步的處理可以將誤差模型、誤差元素等以配置文件的方式引入數控系統,通用性較好。此外,與傳統的基于數控系統的硬件補償方法不同,該補償方法不采用硬件接口,不需要引進相應的硬件設施,而是通過軟件接口進行通信實現各項功能,可靠性更高。
基于數控系統的補償方法相對于 NC 代碼修正補償來說有其獨特的優越性。假定 2 種補償方法的加工條件一致,下面具體分析 2 種補償方案的補償精度。
基于 NC 代碼修正的補償,其補償值反映在 NC 加工文件中的坐標點上。在 NC 文件中,每一行代碼中的坐標點都是該段直線( 圓弧) 的終點,同時也是下段直線( 圓弧) 的起點,采用這種補償方式只是對每段線的起點和終點的修正,沒有考慮中間點的誤差,在執行 NC 文件時采用誤差均勻化的方法折合成該點的誤差量。基于數控系統的嵌入式補償,在數控系統的數據流中反映補償值,該數據流是對 NC 文件實施預處理、刀補、軌跡規劃等一系列操作后的細密數據,能盡可能多的考慮到加工過程中的數據點。如圖 4 所示,xy 平面( G17) 上的半圓弧為例,其中點( x0,y0) 代表圓弧的圓心位置,點( x1,y1) 代表圓弧的起點,點( x2,y2) 代表圓弧的終點位置,R 代表圓弧的半徑,( x0’,y0’) 和( x2’,y2’) 代表補償后的圓弧圓心和終點坐標。圖4(a) 是基于 NC 代碼修正的補償,由圖可知每段代碼只是補償該段代碼的終點; 圖 4( b) 是基于數控系統的補償,由圖可知補償位置點細密,考慮到了圓弧中盡可能多的位置點。
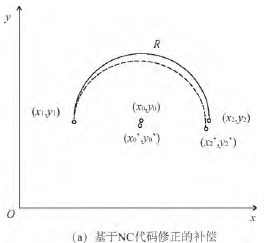
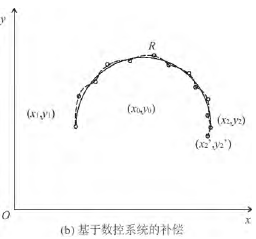
圖 4 2 種補償方法的對比
綜合上述的分析,可知 2 種補償方案都具有各自的特點,如表1所示.
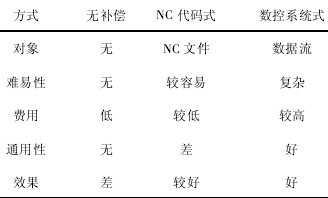
表 1 誤差補償方法的比較
3 、基于 SKY 數控系統的實驗驗證
SKY 數控系統是基于 PMAC 運動控制卡的開放式數控系統。對文中提出的誤差補償方法的補償效果進行驗證,設計了實驗方案以驗證所提出的補償方法的有效性。
a) 實驗方案設計
為了達到驗證誤差補償方法有效性的目的,實驗方案設計如下: 實驗對比環境需要有 2 組,一組為無補償與軟件式補償的對比,另一組為無補償和數控系統式補償的對比。
為了盡量避免外部因素的影響,實驗不進行零件的實際加工,以免引入切削力引起的誤差; 由于機床各個軸系的運動均能反映誤差補償方法的有效性,為了簡化工作量,僅對單軸方向的線性誤差進行測量。同時考慮到誤差檢測的可靠性和準確性,實驗選取激光干涉儀檢測機床線性誤差。
b) 實驗條件和實驗步驟
實驗的對比環境分為 2 組,為“無補償+軟件式補償”和“無補償+數控系統式補償”; 實驗的待檢測機床為具備上述對比環境的 SKY-DX70100 型數控機床; 檢測的目標數據為機床 x 軸向的線性誤差; 誤差檢測儀器為雷尼紹激光干涉儀。
激光干涉儀檢測 x 向誤差時,需要驅動機床沿 x 向在固定范圍內往復運動。誤差檢測時的數控程序如下:
G92 X0 Y0 Z0;
M98 P100 L11;
M98 P200 L12;
M98 P100 L12;
M98 P200 L12;
M02;
: O100
G90 G00;
G91 G00 X-50;
G04 X3;
M99;
: O200
G90 G00;
G91 G00 X+50;
G04 X3;
M99;
其中: G92 為坐標系設定指令; M98 為子程序調用指令,P 表示調用的子程序編號,L 表示調用次數; G04 為等待指令,X 的數值表示等待的時間; : O100 和: O200 為子程序編號; M02 表示程序結束,其余指令的功能與標準數控代碼一致。
實驗步驟如下:
1) 分別在不進行機床誤差補償、采用軟件式補償策略和采用數控系統式補償的條件下,采用激光干涉儀對指定數控機床的 x 軸向線性誤差進行測量,測量結果分別為X_Data1.rtl、X_Data2rtl、X_Data3.rtl 文件;
2) 驗證補償策略的有效性;
3) 實驗結果分析和討論。根據測量結果 X_Data1.rtl、X_Data2.rtl 和 X_Data3.rtl,可以得到未補償時機床 x 軸向的線性誤差范圍為( -76.0μm,8.6 μm) ; 采用補償軟件后機床的 x 軸向線性誤差范圍為( -10.8 μm,-2.0 μm) ; 補償功能與數控系統集成后機床的 x 軸向線性誤差范圍為( -6.8 μm,1.1 μm) 。根據 GB/T17421.2-2000 標準分析測量結果 X_Data1.rtl、X_Data2.rtl 和 X_Data3.rtl,得到該機床 3 種條件下的 x軸向線性誤差曲線如圖 5、圖 6 和圖 7 所示。對比圖 5 和圖 6 可知,相對于未補償時的 x 軸線性誤差曲線,采用誤差補償軟件后,線性誤差的范圍大大縮小,由原來的 84.6 μm 減少到 8.8 μm,降低了 89.6%。對比圖5 和圖 7 可知,當補償功能與數控系統集成后,x 軸的線性誤差曲線的誤差范圍也大大縮小,由原來的 84.6 μm 減少到 7.9 μm,降低了 90.7%。幾種補償條件下 x 軸線性誤差相關參數的比較如表 3 所示。
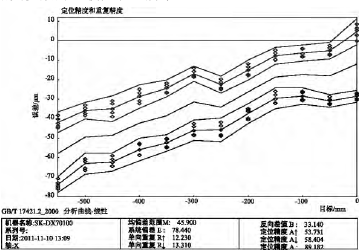
圖 5 無補償條件下機床 x 軸向線性誤差圖
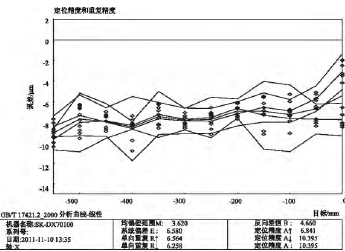
圖 6 軟件式補償條件下機床 x 軸向線性誤差圖
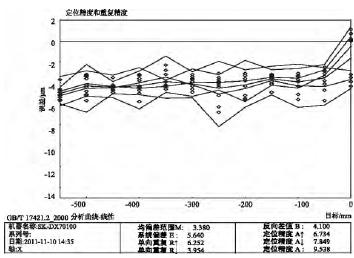
圖 7 數控系統式補償條件下機床 x 軸向線性誤差圖
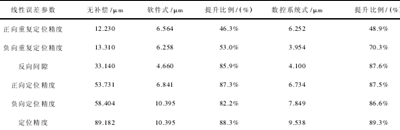
表 3 不同補償時 x 軸線性誤差分析表
根據上述分析可知,采用基于補償軟件與數控系統通信的補償方法和補償功能與數控系統集成的補償方法都大幅度降低了機床的 x 軸向線性誤差,因此,論文提出的補償方法能有效地提高機床的性能。
4 、結語
通過對數控機床常用的空間誤差補償方法進行分析,提出了一種基于數控系統插補數據的誤差補償新方法,實現誤差補償功能與數控系統的集成。根據實驗結果可知,采用補償軟件與數控系統通信的補償方法、補償功能與數控系統集成的補償方法均能大幅度改善機床的性能,為設計開發精密數控機床提供了一條可行的路徑。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息





