加工中心部件故障相關度評估
2018-5-18 來源: 機械科學與工程學院,長春工業大學 作者: 龍 哲,申桂香,張英芝,曾文彬,榮 峰
摘要: 為實現加工中心系統部件間故障相關度評估,采用相關故障機理分析與圖論相結合建立系統部件故障傳遞有向圖的方法,將系統部件相關度評估轉化為復雜網絡節點重要度計算,進而由鄰接矩陣及其轉置變換并結合 pagerank 算法,實現加工中心系統部件故障相關度求解. 計算結果表明: 故障相關度的大小與部件間故障關聯關系成正比,存在故障相關的部件的故障相關度大于不存在故障相關的部件的故障相關度. 若部件被影響度大,影響度小,說明該部件是故障表象部件; 反之,響度大而被影響度小的是故障源部件. 提出的方法有助于故障診斷與維護.
關鍵詞: 加工中心; 部件; 關聯故障; 故障相關度; pagerank 算法
加工中心功能先進性及其結構復雜性,導致系統故障存在相關性,使系統多模、連鎖故障頻率有增加趨勢. 早在 50 年代,在核反應堆設計和操作的初始階段就發現了相關失效現象,1962 年 Lennox 等將其稱為交叉揺合故障. 相關失效分析主要包括定性分析和定量計算. 定性分析常用方法是顯示模型法,如事件樹、故障樹、因果表等; 定量計算主要指參數模型,如 B 因子模型、C 因子模型、基本參數( BP)模型、a 因子模型、多希臘字母( MGL) 模型等數,但這些定量模型多以共因失效為主. Pickles借助Domino 骨牌將獨立的可靠性評價擴展成連續失效過程,借助指定的系數來刻畫某一子系統故障對其相鄰子系統的影響,但因假定的失效序列比較單一.
無法適用于故障的多路徑傳遞方式; Sun 等構建了定量化分析關聯故障的可靠性模型,并結合故障數據計算子系統的相關系數,但是該相關系數是一個綜合指標. 很多學者借助 Copula 函數來研究故障相關性問題,文獻用 Gumbel Copula 函數建立數控裝備部件故障間函數關系,但無法體現相關關系的作用方向. 還有一些學者應用復雜系統相關理論對連鎖關聯故障進行研究,主要包含兩個方面:
一是基于復雜網絡理論的“小世界網絡”模型、Watts 構造模型、Holme 等的相隔中心性模型、Motter 與 Lai 模型等進行連鎖關聯故障機理分析; 二是利用 Monte Carlo 模擬法、遞歸算法、基于 AHP 和灰色關聯度選擇故障序列等進行連鎖關聯故障路徑搜索. 加工中心部件相關故障是連鎖故障類型,且不存在冗余,因此,不能直接照搬電力系統連鎖故障分析及相關度計算方法.
本文將相關故障機理分析與圖論相結合,建立系統部件故障傳遞有向圖,使系統部件相關度評估轉化為復雜網絡節點重要度計算,由鄰接矩陣及其轉置變換并結合 Pagerank 算法,實現加工中心系統
部件故障相關度求解.
1、系統關聯故障建模與評估原理
工程實際中,系統部件的故障事件可能從系統中某一故障源開始,繼而引發系列元件故障,這種關聯故障的迅速傳播最終導致系統崩潰. 本文引入圖論構建系統部件故障傳遞有向圖模型,將部件節點相關度轉化為節點重要度. 應用鄰接矩陣量化圖中節點關聯關系,鄰接矩陣歸一及轉置變換形成系統狀態轉移矩陣,結合 pagerank 算法實現故障傳遞有向圖中節點相關度計算.建模與評估流程如圖
1 所示.
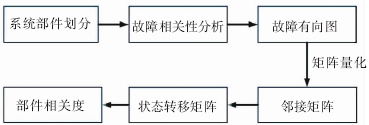
圖 1 關聯故障建模與評估流程
1.1 系統部件關聯故障建模
故障傳遞有向圖是將系統中各元件或子系統簡化為圖中的節點,單元間的故障傳遞關系則被簡化為節點之間的有向邊,依據系統各個元件或單元之間的故障相關關系,構建整個系統的故障有向傳遞模型
. 如果單元 i 出現故障會引發單元 j 出現故障,則存在從節點 i 到節點 j 的一條有向邊.

1.2 基于 pagerank 算法的部件相關度評估
pagerank 算法原理: 若部件 M 故障導致部件 N故障,則可認為部件 M 傳遞給部件 N 一個重要度 p值,此值的大小取決于部件 M 的重要度 p( M) 以及出鏈數. 設任何部件的重要度都被平均傳遞到它所鏈接的部件. 由于部件故障之間存在相互鏈接關系,這個過程會一直迭代下去,最后部件重要度根據故障部件迭代后 p 值進行排序.
基于這一思想,將整個系統抽象成一個有向圖G = ( V,E) ,其中將 n 個部件抽象成網絡節點,節點集合為 V,部件間關系抽象成有向邊,有向邊集合為E. 若鏈入部件 M 的故障節點是部件 V1,V2
,…,Vk,那么部件 M 的重要度為


系統部件間相關度分為影響度與被影響度.
1) 被影響度計算. 基于 pagerank 算法來計算系統部件的被影響度是基于以下假設:
假設 1 系統部件故障以概率 d 出現故障傳遞現象,即沿著故障傳遞模型進行傳遞,其中 0 <d < 1;
假設 2 當系統以概率 (1-d) 不沿故障鏈傳遞,那么下一個故障將以等可能概率發生于任何一個系統部件,系統部件的 CK值將會平均傳遞到各個系統部件;
假設 3 當系統部件 Vi能夠將故障傳遞到部件M,部件 M 會獲得故障相關被影響度 CK( M) ,傳遞值的大小依賴于部件 Vi的出度和其本身的 CK(Vi)值;
假設 4 如果部件容易受到其他 CK值較高的系統部件故障的影響,那么此系統部件的 CK值也會越高.
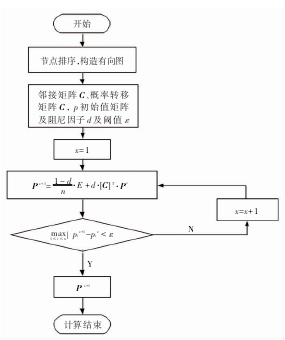
圖 2 Pagerank 算法實現流程

2) 影響度計算. 在故障傳遞過程中,影響度是指系統部件能夠對其他系統部件傳遞故障的能力,是與系統部件出度正相關的,記為 CI,節點出度越大,相應 CI值也越大. CI值代表了系統部件對其它部件產生故障影響的概率. 所以通過對鄰接矩陣進行轉置,借助 pagerank 算法可以求得系統部件故障相關影響度 CI.

2、 加工中心系統部件相關度評估
2.1 加工中心系統關聯故障建模
加工中心系統功能關系如圖 3 所示.
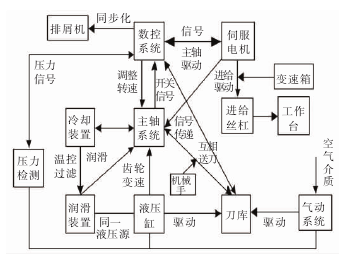
圖 3 加工中心系統功能關系
加工中心系統及部件劃分如表 1 所示.

表 1 加工中心系統故障部件劃分
通過對某型加工中心現場故障數據分析,獲得加工中心部分關聯故障,其關聯故障分析與統計如表 2、3 所示.
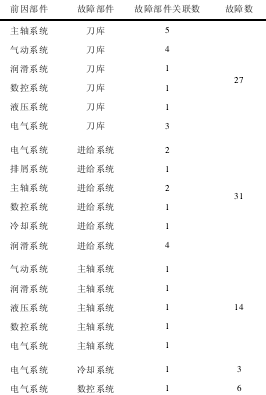
表 2 加工中心關聯故障統計

表 3 加工中心關聯故障分析
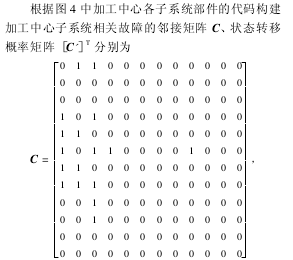
根據表 3 的加工中心關聯故障分析構建故障傳遞關系模型如圖 4 所示.
圖 4 加工中心故障傳遞有向圖模型
2.2 加工中心系統部件故障相關度評估


由表 4 和表 5 可知,進給系統、刀庫和主軸系統的被影響度比較高,容易受其他子系統故障影響;氣系統、潤滑系統、液壓系統、氣動系統等子系統的影響度比較高,當這些子系統出現故障時容易影響其他子系統,對整個加工中心具有較強的危害性.
表 4 子系統 CK值及排序
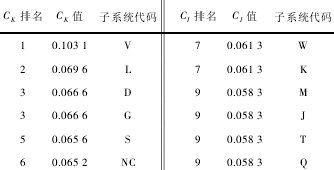
表 5 子系統 CI值及排序
3 、結 論
1) 故障相關度的大小與部件間故障關聯關系成正比,存在故障相關關系的部件的故障相關度大于不存在故障相關關系的部件的故障相關度;
2) 故障相關度反映部件在故障傳遞中的位置.若部件被影響度大,影響度小,說明其是故障表象部件; 反之,影響度大而被影響度小的是故障源部件,這有助于故障診斷與維護.
3) 通過對某加工中心相關故障數據分析發現,進給系統、刀庫和主軸系統的被影響度比較高,這些子系統屬于執行機構,是故障表象子系統; 電氣系統、潤滑系統、液壓系統、氣動系統等子系統的影響度比較高,它們屬于動力或控制系統,屬于故障源子系統. 這與故障相關性定性分析結果一致,說明該方法是合理有效的.
4) 基于 Pagerank 算法的子系統相關度計算,能夠定量評價系統部件故障相關度,為后續的系統部件故障率計算、可靠性評價及可靠性分配等研究奠定理論基礎.
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com





