数控机床市场网-专业的数控机床网站

       摘　要：針對由離散刀位點數據生成的五軸加工等距非均勻有理Ｂ樣條曲線刀具路徑中兩條非均勻有理Ｂ樣條曲線參數不同步的問題，建立了一種等距雙非均勻有理Ｂ樣條曲線參數的同步模型，實現等距雙非均勻有理Ｂ樣條曲線刀具路徑插補過程中兩條非均勻有理Ｂ樣條曲線參數的同步運動。將三軸非均勻有理Ｂ樣條曲線插補算法應用于五軸加工等距雙非均勻有理Ｂ樣條曲線刀具路徑中的刀具中心點非均勻有理Ｂ樣條曲線，根據參數同步模型將插補算法同步到刀軸點非均勻有理Ｂ樣條曲線中。仿真表明，采用該算法能夠使刀具始終沿著等距雙非均勻有理Ｂ樣條曲線刀路進行同步插補，參數同步插補精度主要集中在１０－６　ｍｍ級數上，適用于復雜曲面的五軸加工。

       關鍵詞：五軸加工；等距雙非均勻有理Ｂ樣條曲線；參數同步；插補算法

       ０　引言

      隨著航空航天、國防、運載工具、動力、裝備等行業的飛速發展，由裁剪曲面、組合曲面和流行網格等復雜曲面構成的薄壁零件被廣泛應用，如螺旋槳、整體葉輪以及汽車覆蓋件精密模具等。五軸加工以其高速高精度的特點被廣泛應用于該類自由曲面零件加工［１］。五軸加工刀具軌跡是影響加工效率和加工質量的重要因素，并直接影響刀具壽命和機床損耗［２］，復雜曲面的零件通常對精度要求高、加工工藝性差，在切削力等因素的作用下，容易發生加工變形和切削振動。因此，獲得高質量的刀具路徑不但可以提高加工過程的平穩性、減少機床頻繁加減速從而提高整個加工的切削效率，縮短加工時間，而且可以大大提高曲面的加工精度及光順性、減少后續工序的工作量。

      為獲得高品質的五軸加工刀具路徑，近些年來許多國內外學者對五軸加工雙非均勻有理Ｂ樣條曲線（Ｎｏｎ－Ｕｎｉｆｏｒｍ　Ｒａｔｉｏｎａｌ　Ｂ－Ｓｐｌｉｎｅ　ｃｕｒｖｅ，ＮＵＲＢＳ）刀具路徑的規劃進行了深入研究。Ｌａｎｇｅｒｏｎ等［３］提出了分別對刀具中心點和刀軸點進行ＮＵＲＢＳ來擬合獲取雙ＮＵＲＢＳ曲線刀具路徑的方法，但使用所提方法生成的雙ＮＵＲＢＳ刀路并不等距。通過等距雙ＮＵＲＢＳ刀路能夠確定唯一的刀具姿態，因而能獲得更加光順且精度更高的加工路徑，實現高速平滑加工。基于此，Ｂｉ等［４］提出一種等距雙ＮＵＲＢＳ路徑的生成算法，利用四元數來描述刀具運動，分別擬合生成雙ＮＵＲＢＳ刀路。Ｙｕｅｎ等［５］通過計算機輔助制造（Ｃｏｍｐｕｔｅｒ　Ａｉｄｅｄ　Ｍａｎｕｆａｃｔｕｒｉｎｇ，ＣＡＭ）系統獲得刀具中心點和刀軸矢量數據，將其分別擬合成五次樣條曲線，然后將各樣條曲線重新參數化，以獲得足夠光順的樣條曲線刀具路徑。楊堂勇等［６］針對等距雙ＮＵＲＢＳ刀具路徑中不滿足精度的特點，給出了一種對偶四元數Ｂｅｚｉｅｒ矢量函數的光順方法。通過研究發現，先前的生成雙ＮＵＲＢＳ刀路的方法中，在生成刀具中心點和刀軸點曲線時都使用了同一個參數ｕ。由于生成兩條曲線的離散數據點不同，由累積弦長參數化等參數化方法得到的兩組節點向量勢必不同，如果使用同一個節點向量進行擬合，則將導致另一條曲線的擬合精度下降，從而降低刀具路徑插補的精度。因此，為了獲得更高的加工精度，在擬合雙ＮＵＲＢＳ曲線時應使用不同參數。

      本文針對刀具中心點的曲線參數和刀軸點的曲線參數不相同這一特點，構建了一個雙ＮＵＲＢＳ曲線參數同步模型，使得給出任意一個刀具中心點曲線的參數值都能得出刀軸點曲線的參數值，以解決刀具中心點曲線和刀軸點曲線的參數同步問題，并應用該模型實現等距雙ＮＵＲＢＳ刀具路徑的同步插補。

     １　、五軸等距雙ＮＵＲＢＳ刀具路徑生成

     不同于三軸加工刀具路徑，五軸加工的刀具路徑不僅包含刀具中心點，還包含刀軸矢量信息。五軸等距雙ＮＵＲＢＳ刀具路徑中的一條為刀具中心點ＮＵＲＢＳ曲線，另一條為刀軸上某點的ＮＵＲＢＳ曲線，如圖１所示。任意時刻，通過對應的刀具中心點與刀軸點即可確定刀軸矢量。

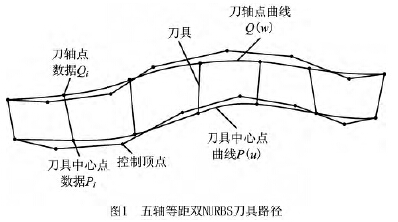
     將有序的離散刀位點數據進行ＮＵＲＢＳ曲線插值，其主要目的是求節點矢量和控制頂點。為簡化運算，將權重ωｉ賦值為１，此時ＮＵＲＢＳ曲線可簡化為Ｂ樣條曲線計算。由于高次插值曲線存在難以給出的邊界條件，實踐中廣泛采用Ｃ２ 連續的三次Ｂ樣條曲線作為插值曲線［７］。

   
     １．１　刀具中心點ＮＵＲＢＳ曲線的生成

      三次Ｂ樣條曲線可定義為：

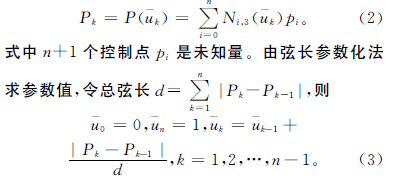
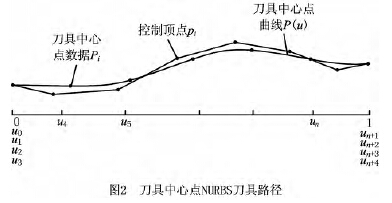
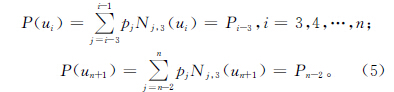
      式中含ｎ－１個方程與ｎ＋１個未知頂點。對于Ｃ２連續的三次Ｂ樣條閉曲線，因具有周期性，首末數據點相重，不計重復，方程數減少一個。ｎ＋１個頂點中的首末三個依次相重：ｐ０＝ｐｎ，ｐ１＝ｐｎ＋１，ｐ２＝ｐｎ＋２，未知數頂點減少到ｎ－２個。因此，可從ｎ－２個方程中求解出ｎ－２個未知頂點。上述方程組可寫成下列矩陣形式：

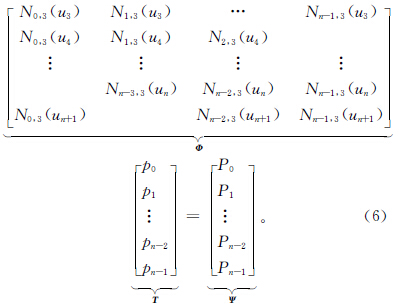
　    刀軸點ＮＵＲＢＳ曲線的生成

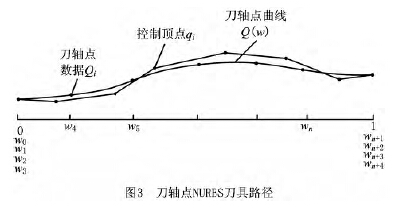
      圖３為刀軸點的刀具路徑示意圖，給定的離散刀位點數據為一系列刀具中心點數據Ｐｉ和刀軸矢量數據Ｏｉ，已知刀具為剛體，則刀具上某點到刀具中心點的距離Ｈ 是一定的，因此刀具上某點的數據可以表示為

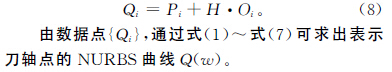
      ２　、等距雙ＮＵＲＢＳ曲線參數關系模型

      五軸加工時刀具的運動不僅要保證刀具中心點的速度平滑，還要保證刀軸矢量轉動的速度平滑，而刀軸矢量轉動的速度平滑可以通過刀軸上某點的速度平滑來保證。等距雙ＮＵＲＢＳ刀具路徑中刀具中心點與刀軸點的距離為一固定值Ｈ，分析五軸聯動雙ＮＵＲＢＳ 刀具運動軌跡可知，刀具中心點ＮＵＲＢＳ曲線Ｐ（ｕ）與刀軸點ＮＵＲＢＳ曲線Ｑ（ｗ）是平行并列關系，對任意時刻曲線Ｐ（ｕ）的參數值ｕ∈［ｕｋ，ｕｋ＋１］時，都有曲線Ｑ（ｗ）的參數值ｗ∈［ｗｋ，ｗｋ＋１］。為保證刀具沿兩條ＮＵＲＢＳ曲線同步平滑運動，推導出任一瞬時兩ＮＵＲＢＳ曲線之間的關系，并建立兩ＮＵＲＢＳ曲線的參數關系模型，如圖４所示。

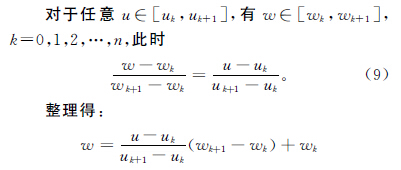
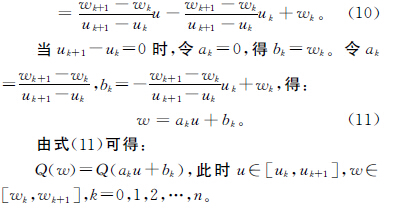
      在刀具中心點ＮＵＲＢＳ曲線Ｐ（ｕ）上任取一個參數值ｕ，都能在刀軸點曲線Ｑ（ｗ）上找到一個參數值ｗ＝ａｋｕ＋ｂｋ與之對應。

      ３　、五軸等距雙ＮＵＲＢＳ刀具路徑同步插補

      不同于三軸加工ＮＵＲＢＳ刀具路徑的插補，五軸加工等距雙ＮＵＲＢＳ刀具路徑的插補不僅要考慮刀具中心點的插補，還要考慮刀軸矢量的插補，而刀軸矢量的插補比較困難。本文先求刀具中心點曲線Ｐ（ｕ）的下一插補點參數值，再由兩ＮＵＲＢＳ曲線參數關系推導出刀軸點曲線Ｑ（ｗ）下一插補點的參數值。圖５所示為五軸等距雙ＮＵＲＢＳ曲線插補示意圖。

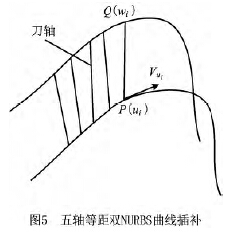
      由泰勒二階展開法，得刀具中心點曲線Ｐ（ｕ）下一插補點的參數值

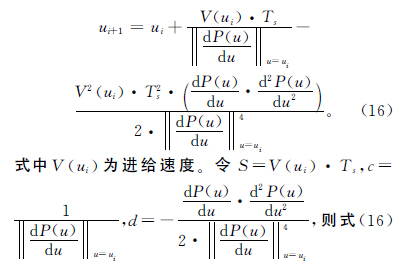
       ４　、算例仿真

       本文采用基體高為９３ｍｍ、直徑為３７２．６９ｍｍ的葉輪進行仿真驗證，建模仿真如圖６所示。仿真算例驗證了本文所提同步插補算法的有效性，能夠對加工葉輪葉片的線性刀路進行光順擬合，生成達到Ｇ１ 以上連續的等距雙ＮＵＲＢＳ刀具路徑，保證插補過程中的任意時刻均能保持等距，實現高速平滑加工。

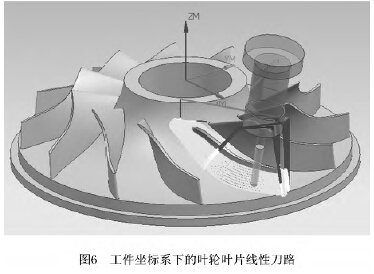
      由ＣＡＭ 加工模塊獲取工件坐標下葉片模型的刀位點數據為一系列ＧＯＴＯ語句：

       其中，前三列為刀具中心點數據Ｐｉ，后三列為刀軸單位矢量數據Ｏｉ。由刀位點數據Ｐｉ和Ｏｉ，得到刀軸上某點的數據Ｑｉ＝Ｐｉ＋Ｈ·Ｏｉ，設置刀具中心點與刀軸點的距離Ｈ＝２０ｍｍ。將數據Ｐｉ和Ｏｉ分別進行三次ＮＵＲＢＳ插值，并采用文獻［９］給出的方法計算雙ＮＵＲＢＳ刀路的擬合誤差，以獲得滿足精度要求的兩條ＮＵＲＢＳ曲線Ｐ（ｕ）和Ｑ（ｗ），最后對等距雙ＮＵＲＢＳ刀具路徑進行同步插補。為便于仿真計算，將ＮＵＲＢＳ曲線的權重ωｉ賦值為１，應用的插補算法是三軸ＮＵＲＢＳ插補中常用的泰勒二階展開法。

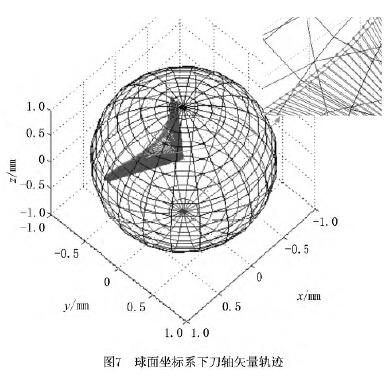
      由ＭＡＴＬＡＢ進行仿真驗證可得圖７～圖１０，圖７為球面坐標系下刀軸矢量軌跡的仿真圖，如圖可見刀軸矢量光滑地分布在球面上，表明擬合光順性較好；圖８是在ＭＡＴＬＡＢ軟件下插值生成的五軸加工等距雙ＮＵＲＢＳ刀具路徑仿真圖，圖中的兩條ＮＵＲＢＳ曲線的任意對應點的間距都是Ｈ ＝２０ｍｍ；圖９為五軸等距雙ＮＵＲＢＳ刀具路徑的運行軌跡仿真圖，直觀地展現了刀具任意時刻的位置和姿態；圖１０為等距雙ＮＵＲＢＳ插補圖，由圖８插補仿真而來。

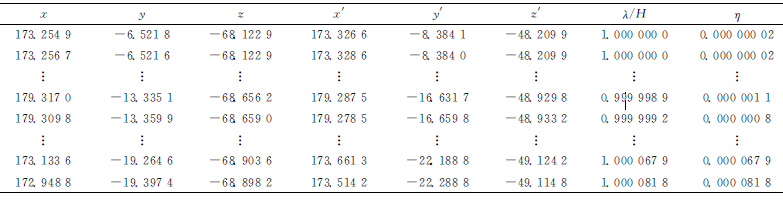
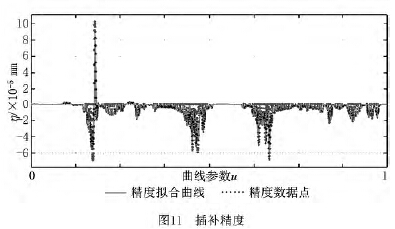
      設（ｘ，ｙ，ｚ）為刀具中心點ＮＵＲＢＳ曲線上的插補點，（ｘ′，ｙ′，ｚ′）為對應的刀軸點ＮＵＲＢＳ曲線上的插補點，      ，則λ表示兩點間的距離，η 表示刀軸矢量偏移量即插補精度。表１給出了部分等距雙ＮＵＲＢＳ刀具路徑的插補數據，λ／Ｈ 為兩條ＮＵＲＢＳ曲線上的插補點間距的模，η＝λ／Ｈ－１為插補精度。如圖１１的插補精度中，數據點表示插補精度η，精度曲線由η擬合得到，表示插補精度的大小。從圖１１可以看出，插補精度η 的值在１０－５　ｍｍ 的級數以下且主要集中在１０－６　ｍｍ的級數上，算法的插補精度較高，表明采用本文算法能夠使刀具始終沿著等距的雙ＮＵＲＢＳ刀路進行同步插補，能獲得更加光順且精度更高的加工路徑，從而使零件表面的加工質量更好。

 
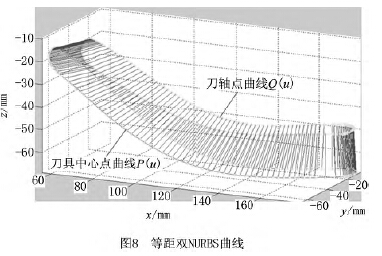
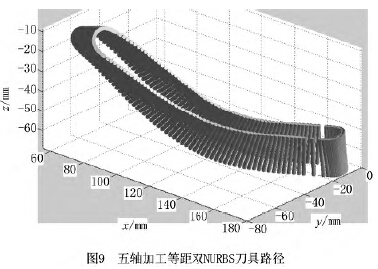
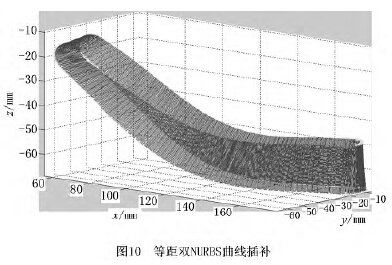
表１　等距雙ＮＵＲＢＳ刀具路徑插補數據

       ５　、結束語

       本文提出一種構建等距雙ＮＵＲＢＳ曲線參數同步關系模型的算法，針對工件坐標系下的離散線性刀路進行光順，以獲取滿足給定精度且達到Ｇ１ 以上連續的等距雙ＮＵＲＢＳ刀具路徑，并實現高精度的同步插補。首先獲取刀位點數據并進行三次ＮＵＲＢＳ曲線插值，生成等距雙ＮＵＲＢＳ曲線刀具路徑；然后分析五軸加工等距雙ＮＵＲＢＳ刀路運動軌跡，推出任一瞬時兩條ＮＵＲＢＳ曲線之間的關系，并建立兩條ＮＵＲＢＳ曲線參數同步關系模型；最后根據三軸ＮＵＲＢＳ曲線插補算法求出刀具中心點曲線Ｐ（ｕ）下一插補點的參數值，并通過曲線參數關系推出對應的刀軸點曲線Ｑ（ｗ）下一插補點的參數值。仿真算例表明，所提算法可以生成等距雙ＮＵＲＢＳ刀具路徑且參數同步插補模型精度在１０－５　ｍｍ級數以下并主要集中在１０－６　ｍｍ級數上。因此，算法的插補精度較高，適用于復雜曲面的五軸加工中。本文的等距雙ＮＵＲＢＳ刀路同步插補算法，并未考慮機床運動學與動力學等約束。因此，可進一步研究機床運動學與動力學等約束下的五軸聯動插補算法和機床各軸伺服能力約束下的進給速度、進給加速度的規劃問題。