摘要: 應用Soildworks 建立高效立式加工中心立柱數字化模型,運用Simulation 對立柱進行有限元分析,獲得立柱的靜、動態特性參數。綜合運用正交試驗設計、模糊數學和有限元分析理論,對立柱的結構參數進行多目標模糊優化,獲得最優結構參數為壁厚22 mm、肋板厚18 mm、頂部開窗大小140 mm×320 mm。分析表明,優化后立柱位移減小6%,1 階固有頻率增加1.2%。通過對立柱結構參數的優化,提高了其靜、動態特性。
1 、立柱結構模型的建立
采用三維建模軟件Solidworks 建立加工中心立柱數字化模型,并且為了能方便地在進行結構分析時獲得有效地計算結果,同時又能保證分析速度以及分析精度,首先對立柱模型進行結構簡化,去掉立柱結構中對分析影響不大的凸臺、螺紋孔以及倒角,進而得到簡化的立柱數字化模型,如圖1 所示*河北省科技支撐計劃資助項目(11212110D) 。

圖1 立柱數字化模型
2 、立柱靜、動態性能分析
(1)單元選取及網格劃分
立柱的參數設定:材料為HT250,各向同性,介質均勻,彈性模量E=130 GPa,泊松比γ=0.25,密度ρ=7.4 g/mm3,由于加工中心立柱的結構復雜,所以網格劃分將采用Solidworks Simulation 中網格智能劃分方法,同時為了能夠減少單元數量,提高分析速度,選用高品質單元,劃分后節點總數為93 626,單元數為52 494。
(2)立柱的靜態分析
靜態分析是計算在固定載荷作用下結構產生的位移、應力以及應變,而且不需要考慮慣性和阻尼的影響。在進行有限元分析時約束施加在立柱底部與床身接觸的4 個方形區域,立柱所受工作載荷主要是主軸箱的重力和切削力。以鉆孔為典型工況,立柱受力如圖2 所示,沿X 軸方向的載荷分別為:Fx1=Fx2=177.9 N、Fx3=Fx4=233.1 N, 沿Y 軸方向的
載荷分別為:Fy1=Fy2=277.1 N、Fy3=Fy4=-266.1 N,以及沿Z 軸方向的載荷Fz=271.4 N。
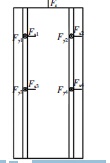
圖2 立柱受力圖
將數字化模型導入Solidworks Simulation,便可進行求解運算,求解后的立柱位移云圖如圖3、圖4所示。由圖3、圖4 可以看出X 向位移變化量最大,其最大變形量為6.55e-4 mm,并且發生在立柱的垂直壁上,而Y 向變形較小,可以忽略,因此可以通過改變肋板厚、立柱壁厚以及改變肋板布局來提高立柱的剛度。
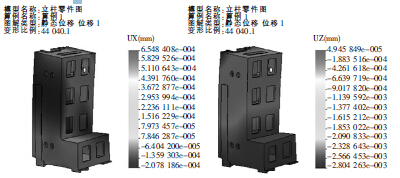
圖3 X 向變形量 圖4 Y 向變形量
(3)立柱的動態分析
動態性能分析可以反映出結構的2 個振動特性參數,即固有頻率和振型,這2 個特性是動態分析中2 個重要的參數,因在動態性能分析中與載荷無關,因而能夠充分體現結構特性,并且可以從分析結果中看出其結構的薄弱環節,從而為結構優化提供依據。
模態分析中該立柱的約束施加在立柱底部與床身接觸的4 個方形區域。立柱的振動是由各階振型的線性疊加, 其低階振型比高階振型影響大,越是低階影響越大,低階振型對立柱的動態性能起決定作用,因此,取立柱的前5 階模態振型進行動態性能分析。
將數字化模型和約束導入Solidworks Simulation,便可進行求解運算,運行計算后,可得到立柱的前5階固有頻率和振型,如圖5~圖9 所示。

圖5 1 階振型 圖6 2 階振型

圖7 3 階振型 圖8 4 階振型

圖9 5 階振型
由圖5~圖9 可知,前5 階固有頻率分別為146.48Hz、164.43 Hz、300.59 Hz、434.27 Hz、446.24 Hz;第1階振型主要表現為立柱上部沿X 軸搖擺振動; 第2階振型主要表現為立柱上部沿Y 軸搖擺振動; 第3階振型主要表現為立柱沿Z 軸扭轉振動;第4 階振型主要表現為在中間開窗部分做內凹振動;第5 階振型類似于第3 階振型。可見第1、第2、第4 階振型為局部振動,而第3、第5 振型為整體振動。第1、第2 階振型的固有頻率較低,可通過強化立柱剛度來提高的動態性能。
3 、立柱結構參數優化
通過對加工中心立柱的靜、動態性能分析可知,其影響因素主要有立柱的剛度、主軸箱的重量、工況、切削載荷和立柱材料等。若改善立柱的靜、動態性能,最有效的方法就是提高立柱的剛度。
(1)立柱設計方案的確定
立柱的剛度與截面形狀和尺寸有關,而影響立柱的截面形狀和尺寸因素很多,選擇截面形狀和尺寸較優的立柱,就成為一件非常繁瑣的工作。采用正交試驗法,將會降低試驗次數,從而減少一些不必要的工作量。①選擇立柱壁厚、肋板厚、頂部開窗大小作為正交試驗的3 個因素;②根據每一設計參數的范圍內選取3 個不同水平的值;③選取正交試驗表L9(34),由此確定9 個正交設計方案如表1 所示。
表1 正交試驗方案
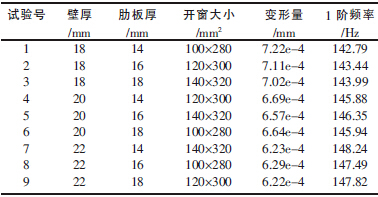
應用Solidworks 分別建立9 個方案的立柱數字化模型,然后導入有限元分析軟件Solidworks Simulation進行求解運算,得出9 個方案立柱的動靜態特性分析結果即變形量與1 階頻率如表1 所示。
(2)立柱參數多目標模糊優化
多目標模糊優化理論是在基于求解各單目標問題滿意解的基礎上尋求多目標最優解,能夠充分體現它們之間的相互關系,可以較好地兼顧多個目標,且各目標之間的相對重要性可以通過權重加以體現。
為了綜合考慮各因素對立柱結構的影響,現以模糊綜合評價值作為綜合評價指標。以變形量、1 階頻率為評價指標集U={Y1,Y2}。以正交試驗設計的9 個設計方案為評價對象集,D={d1,d2,…,d9}。建立評價指標集U 對評價級V 的隸屬函數,使根據隸屬函數計算得到的隸屬度值的大小與該指標在綜合評價中的重要性相適應, 隸屬函數為單調函數,隸屬度rmn在0~1(m=1,2,3),(n=1,2,…,9)。其中,變形量Y1n為偏小型指標, 隸屬函數為r1n =

表2 單指標的隸屬度值和模糊綜合評價值
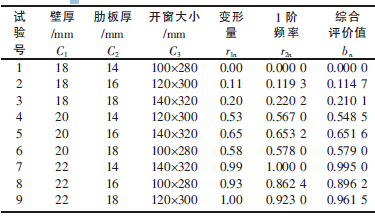
A 是指標集U 上的模糊子集, 稱為權重分配集,它反映各指標的重要程度。在立柱設計中,變形量和1 階頻率直接影響其加工的精度,各取權重為0.5。由此模糊子集A 確定為:A={0.5/Y1,0.5/Y2},簡記為:A={0.5,0.5}。
在評價集V 上引入一個模糊子集B,稱為評價級,它的模糊評價B={b1,b2,…,b9},由模糊矩陣R與權重分配集A 經模糊變換得到:B=AoR。模糊運算方法有多種,采用M(·,+)算子對B=AoR 進行模糊變換, 得到綜合評價模糊子集B 的隸屬度bn,即模糊綜合評價值,如表2 所示。
由主效應分析計算,可知3 個設計參數對立柱綜合性能的影響程度從大到小依次為壁厚、頂部開窗大小、肋板厚;由兩因素之間的交互效應分折可知,壁厚與開窗大小的交互效應最大;由全部因素各水平搭配的交互效應分析可知, 在全部可能的3種因素各水平搭配中,壁厚22 mm、肋板厚18 mm、開窗大小140 mm×320 mm 對綜合評價值的影響最大。
因此在考慮交互作用情況下,這種參數組合得到的綜合評價值最好。
(3)優化后立柱結構性能分析
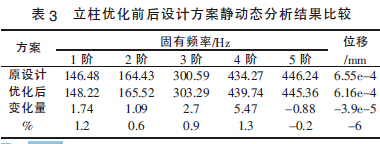
根據模糊綜合評價值最好的立柱設計參數:壁厚22 mm、肋板厚18 mm、開窗大小140 mm×320 mm,應用Solidworks 建立該方案的立柱數字化模型,并導入有限元分析軟件Solidworks Simulation 中進行有限元靜、動態特性分析。根據優化前、后立柱結構的有限元分析結果,將最大變形量、1 階固有頻率幾個最重要的指標匯總如表3 所示。
由表3 結果表明,優化后的立柱結構與優化前設計結構最大位移減小了6%,1 階固有頻率增加了。
4、 結語
應用Simulation 有限元分析軟件, 對所設計的高效立式加工中心立柱進行了靜、動態特性分析,獲得了立柱在不同方向上的受力變形,通過對立柱的固有頻率及振型的分析,獲得了立柱的動態特性參數。綜合運用正交試驗設計、模糊數學和有限元分析理論,對立柱的結構參數進行了多目標模糊優化。分析表明,通過Soildworks Simulation 有限元分析方法對加工中心立柱進行靜、動態特性分析,可以快速有效地確定立柱結構參數的最優方案,縮短產品的試驗周期以及大量的試驗和計算工作, 為機床結構優化設計提供了一種新的途徑。
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com





