機床主軸承多源信息融合故障診斷
2021-1-25 來源：哈爾濱工程大學自動化學院 作者：劉勝，吳迪，李芃
摘要：針對機床主軸承的故障診斷，為解決傳統方法僅由單一傳感器數據分析準確性低的問題，提出基于主元小波包、遞歸神經網絡以及振動及噪聲信號多源數據融合的軸承故障診斷方法，實現對鍛壓機床主軸承的故障診斷。將振動及噪聲傳感器采集的信號，經主元小波包處理提取特征值，再利用遞歸神經網絡進行局部故障診斷，得到不同傳感器對軸承故障互相獨立的故障證據，然后采用基于數據修正 D-S 證據理論將振動及噪聲診斷結果融合，發現基于遞歸神經網絡及數據修正 D-S 證據理論的診斷方法。該方法解決了單一傳感器的不穩定性和局限性以及傳統 D-S 證據理論沖突證據失效的問題，使故障診斷具備容錯能力，提高了傳統故障診斷的精確度。
關鍵詞：機床主軸承；故障診斷；振動噪聲分析；主元小波包；遞歸神經網絡；多源數據融合
1、引言
據統計，機床主軸系統在軸承、主軸、絲杠及皮帶位置處，總計故障率達到 70%，一旦發生故障，機床無法正常工作，甚至對人身安全有嚴重影響，因此，鍛壓機床主軸承的故障診斷有極為重要的意義。鍛壓機床主軸承故障診斷實質上是對機床軸承不同的運行狀態進行識別，首先建立不同狀態分類的特征空間，提取設備振動信號的特征值，將特征信號映射到狀態模式特征空間進行判斷。基于軸承振動信號，小波分析及 BP 神經網絡進行特征分析的方法已經被廣泛用于鍛壓機床主軸承的故障診斷，但單一傳感器工作不具備可靠性及穩定性，容易因傳感器故障產生局部信息偏差或錯誤，最終導致診斷系統的精度下降，甚至誤判。
將機床主軸承振動及噪聲信號通過主元小波包分解為高頻部分和低頻部分，去噪處理，提取軸承頻率特征值，然后通過主元降維，精簡軸承狀態特征值，再用遞歸神經網絡得到局部診斷結果。多源信息融合技術是將類型不同但具有協同作用的傳感器信號，采用某種融合規則，合理分配使用，做出同一環境下具備一致性結論的主軸承狀態特征。本文對機床主軸承的振動及噪聲信號采用基于數據修正 D-S證據理論結合高精度特征值提取及 Elman 網絡的診斷方法，提高神經網絡的局部診斷精度，解決傳統 D-S證據理論對于沖突證據融合失效的問題，最終形成有容錯能力故障診斷方法。
2、機床主軸承狀態特征值分析
2.1、振動及噪聲小波包去噪
對于鍛壓機床主軸承振動及噪聲信號的去噪方法，小波包分解較小波變換更為精細，能夠滿足鍛壓機床信號處理要求。小波包分析實質上是采用基于尺度函數和小波函數導出的低通濾波器和高通濾波器模型，利用小波函數的尺度伸縮平移變換，不斷地將主軸承狀態信號在不同尺度下濾波處理。
設 x(t) 為一時間信號，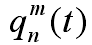
為第 n 層分解上第 m個小波包系數，G 和 H 是與尺度函數及小波函數有關的分頻濾波器，小波包分解與重構算法為：
為第 n 層分解上第 m個小波包系數，G 和 H 是與尺度函數及小波函數有關的分頻濾波器，小波包分解與重構算法為：
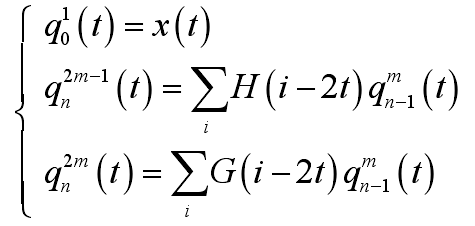
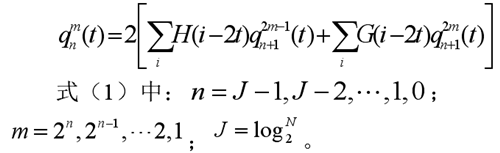
本實驗選取機床主軸軸承作為研究對象，采用CZ891 一體化振動變送器垂直于主軸承安裝，采集振動信號；采用 TK-2KA 噪聲傳感器采集軸承噪聲信號，傳感器安裝位置如圖 1 所示，圖中①、②、③分別為 2個振動傳感器和 1 個噪聲傳感器，采用 LabView2015、NIPXLE-4499 數據采集模塊配合 PXIe-1085 機箱進行振動及噪聲信號采集。
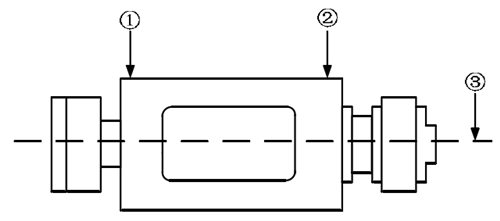
圖1：主軸承傳感器安裝示意圖
調試參數后，選擇 db4 作為小波基，進行 3 層分解，信號采樣頻率為 600Hz，分解后各頻帶對應頻率范圍為[0，37.5]，[37.5，75]，[75，112.5]，[112.5，150]，[150，187.5]，[187.5，225]，[225，262.5]，[262.5，300]的 8 個頻帶。
機床現場環境不封閉，采集的振動及噪聲信號雖具有豐富的信息，但同時存在大量干擾信息，不利于主軸承狀態特征提取，通過小波包去噪及頻帶能量特征提取，可將狀態信號中雜亂無章的部分過濾，處理后信號軸承狀態特征明顯，更具有可靠性。
2.2、主軸承狀態特征值主元分析
主元分析用于降低小波包去噪后主軸承狀態特征值的維數。主元分析最早由 Pearson 提出，是用攜帶足夠多信息且變量維數少的空間反映多變量復雜空間，揭露隱藏在復雜數據內部的簡單結構，對原有數據進行簡化降維的重要手段，廣泛用于過程數據的檢測分析。
其線性代數分析過程是在尋找一組正交基矩陣 P，有 Y=PX，使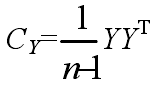
是對角陣，則 P 的行向量就是數據 X 的主元向量，而矩陣 P 就是由主元分析求得的一組正交基構成，P 的行向量是主元分析得到的降維結果。
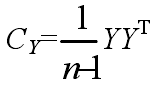是對角陣，則 P 的行向量就是數據 X 的主元向量，而矩陣 P 就是由主元分析求得的一組正交基構成，P 的行向量是主元分析得到的降維結果。 故將主軸承特征頻率構成的向量空間映射到狀態空間，分析狀態類型。主軸在四種工作狀態下采集振動及噪聲信號，將不同情況下的信號經過主元小波包去噪后，在不同頻率下進行峰值提取（其中 f 為工頻），構成 8 維的特征向量，再通過主元降維得到 4 維特征向量，減小 Elman 網絡輸入維度，最后將特征向量歸一化處理，將幾十、幾百的數值降低到小數形式，方便計算，最終得到四種狀態的振動及噪聲的部分特征值如表 1、表 2 所示。
表1：四種鍛壓機床主軸承振動狀態特征值
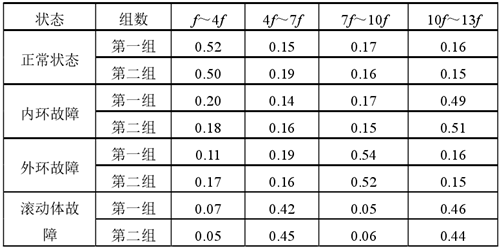
表2：四種鍛壓機床主軸承噪聲狀態特征值
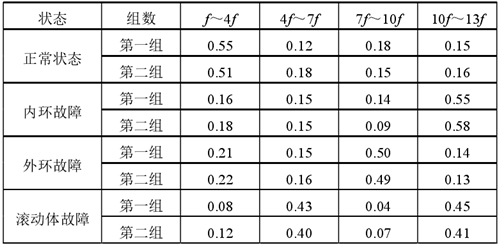
以其中一組狀態特征數據為例，圖 2 是主軸承不同狀態能量特征的頻帶柱狀圖。
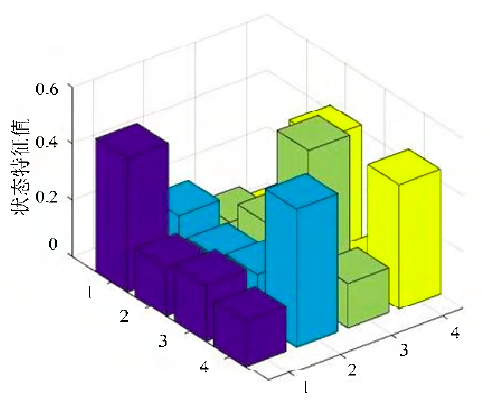
圖2：主軸承狀態頻帶比較
機床主軸承振動及噪聲信號，通過特征提取及歸一化處理后的狀態波形構成 8 維特征向量，經過主元分析后，8 維的特征向量降低到 4 維，用最精簡的維數表示同一種主軸承狀態，便于觀察特征值規律，簡化神經網絡拓撲結構，提高故障診斷效率。
3、主軸承振動及噪聲遞歸神經網絡分析
主元小波包特征提取后，主軸承振動及噪聲信號構成的特征空間作為輸入，采用遞歸神經網絡進行訓練，映射到主軸承狀態空間。選擇 S 激活函數，將 BP或動態反向傳播算法應用于遞歸結構中即組成 Elman網絡；亦可采用基于高斯激活函數的 RBF 訓練權值。
與前饋網絡類似，物理信號由輸入層傳輸，通過特有的上下文單元以及線性或非線性激發函數組成的隱層，最終通過線性加權輸出。而上下文單元類似于一個步時延算子，不斷記憶前一刻的隱層輸出值，其動態學習算法如下：
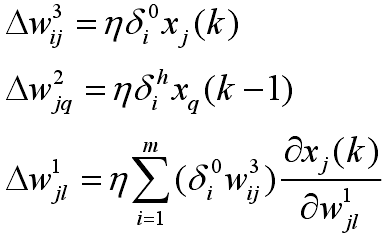
其中：
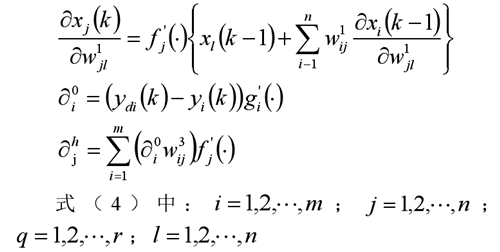
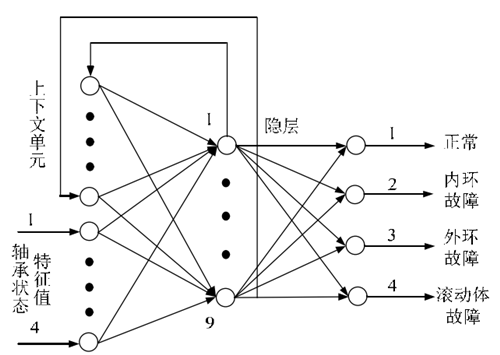
圖3：Elman 網絡模型
將振動及噪聲的特征值作為 Elman 網絡的輸入，設計輸入節點數為 4；隱層節點數為 9；上下文單元與隱層節點數相同；輸出為正常工作及 3 種不同的故障狀態，設計輸出節點為 4，其狀態對應訓練目標輸出為：正常狀態（0001）；軸承內環點蝕（0010）；軸承外環點蝕（0100）；滾動體點蝕（1000），通過參數設計及調整，建立神經網絡模型如圖 3 所示。
4、基于數據修正的主軸承 D-S 證據融合分析
傳統 D-S 證據理論無法解決沖突數據融合失效的問題，文獻應用相似度函數改進 D-S 證據理論，本文基于文獻的相似度函數，但并不采用其支持度和信任度，而是將相似度函數運用在數據預處理中，并通過兩次歸一化過程，保證融合數據和為 1 的性質，再采用 D-S 證據理論將數據融合，簡化了處理過程，提高了數據處理速度，并仍能得到比傳統 D-S 證據理論優秀的融合結果。
將機床主軸承工作狀態作為問題的識別框架，把遞歸神經網絡的局部診斷融合，提高診斷精度。設非空集合 θ 由可窮舉且互斥的基本命題組成，對主軸承中狀態命題 A 都屬于集合★10稱 m 為基本信任分配函數， E(A) 代表命題 A 的證據，定義相似函數及相似度和函數：
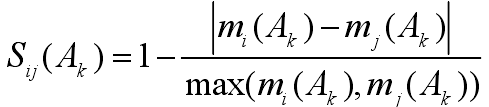
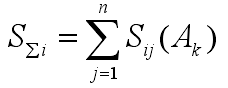
式中：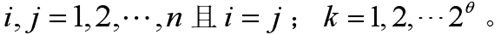
顯然地當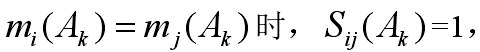
代表證據對命題的判定完全相似。
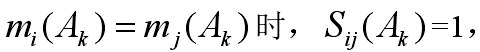顯然地當代表證據對命題的判定完全相似。 定義基于相似度和函數★15的數據修正系數為：
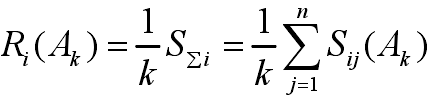
式中：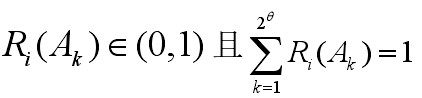
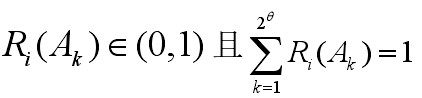
得到數據修正系數修正后的基本信任分配函數如式（7）所示，且易發現★18可以進行下一步融合計算。
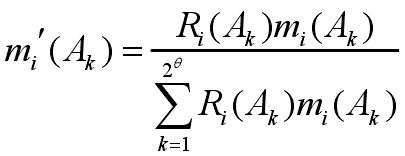
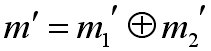稱作 A，B 焦元下新組合的信任分配函數，其表達式為：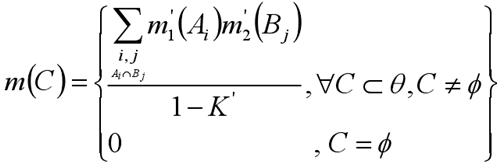 
其中：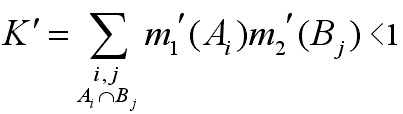
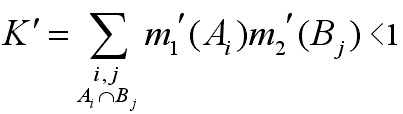
對主軸承振動及噪聲數據逐層修正，再將每次修正后的數據與上一層證據結果融合，證據每一次融合都重新計算相似度及數據修正系數，提高數據的協同性，達到連續提高數據融合精度的效果。
5、鍛壓機床主軸承故障診斷結果
對機床主軸承故障診斷首先要形成狀態映射空間，主軸承狀態類型大體可分為：正常狀態、滾動軸承內環點蝕、滾動軸承外環點蝕、轉動體點蝕四種，其故障特征體現在振動及噪聲頻譜諧波的不同，如下所示：
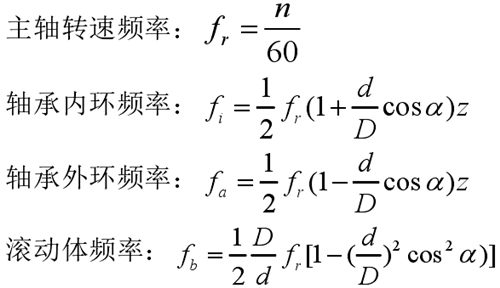
式中：fr 為滾動軸承內圈的回轉頻率；d 為滾動體直徑；D 為軸承半徑；z 為滾動體個數；α 為壓力角。
7016AC 型主軸承參數：d=10mm，D=102.5mm，z=21，α=25°，機床在 1200r/min 工況下采集振動及噪聲信號，噪聲屬于振動同源信號，具有振動的故障頻率特征。經計算，主軸轉速頻率：20Hz；內環故障頻率：228.6Hz；外環故障頻率：191.4Hz；滾動體故障頻率：101.7Hz。通過分析正常及三種故障狀態下頻譜的區別，將頻率范圍作為判斷依據。
獲取四種狀態類型數據各 50 組，共 200 組，就可以組成一個 200×4 的矩陣，以“行”為單位打亂矩陣并選擇前 180 組數據訓練網絡，后 20 組數據作為網絡效果的測試樣本，訓練后發現對應去噪后的振動及噪聲信號。
主軸承振動及噪聲信號屬于高維輸入的特征空間，數據內容豐富，采用傳統的 BP、RBF 網絡容易出現訓練困難、對外部噪聲敏感的弊端，分別將狀態特征值輸入 BP、RBF、Elman 網絡，通過網絡判定的狀態類型分別如圖 3a、圖 3b、圖 3c 所示。
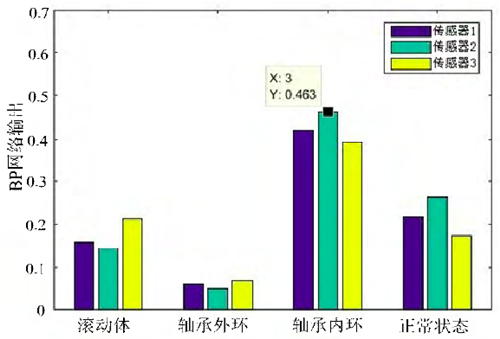
a：BP 網絡診斷結果輸出
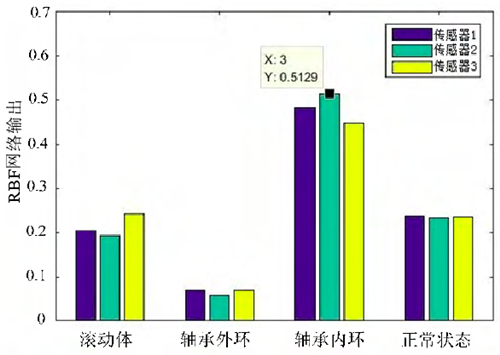
b：RBF 網絡診斷結果輸出
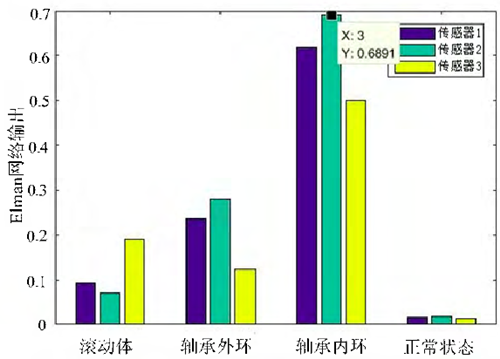
c：Elman 網絡診斷結果輸出
圖3：不同網絡診斷結果輸出
由圖 3 可以看出，此網絡內部多層學習的動態特性，優化了傳統數據的輸入或訓練方式，因此對于主軸故障診斷更具有適應時變特性的能力，與 BP、RBF相比，結果更加精確。
為探究多源數據融合的容錯能力，采用 2 個振動傳感器，1 個噪聲傳感器，其中傳感器網絡的一組輸入特征值數據如表 3 所示。
表3：傳感器網絡輸入特征值
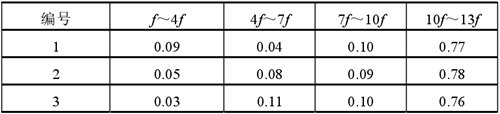
經過歸一化處理及網絡學習后得到網絡狀態輸出向量如表 4 所示。
表4：三個傳感器神經網絡輸出
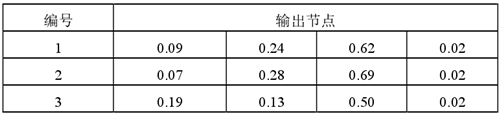
由表 4 可見，理論輸出 1，實際輸出 0.62、0.69、0.50，將輸出歸一化求信任度，證據均指向機床滾動軸承內環點蝕故障狀態，信任度分別達到 0.64、0.65、0.60，如表 5 所示。
表5：故障信任度
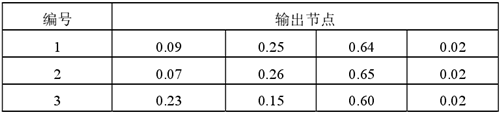
表6：融合前后診斷結果比較
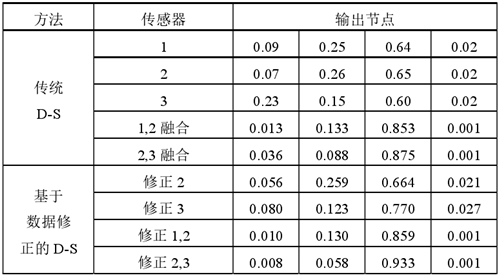
分別采用傳統 D-S 證據理論和基于數據修正的D-S 證據理論將信號融合，前后診斷結果比較如表 6所示。
根據傳統 D-S 證據理論將編號 1 和編號 2 的振動傳感器融合，K=0.5123，然后獲得振動傳感器經過Elman 網絡所確定的可信任分配函數值，再將二者融合狀態類型信任度從 0.64、0.65 提升到 0.853，發現精確度明顯增加。將編號 2、3 采用同樣方法融合，K=0.5545，根據公式求得信任度從 0.853 提升到 0.875，故障診斷信任度增加。
采用本文融合方法，編號 1、2 傳感器數據相似度{0.778，0.962，0.985，1}，基于相似度的修正系數{0.201，0.258，0.264，0.269}，修正后 2 號傳感器數據{0.056，0.259，0.664，0.0201}，計算 K’=0.5049，再將二者融合后的信任度與傳統 D-S 融合結果 0.853相比，信任度提升到0.858。同樣 2、3 傳感器數據相似度{0.244，0.579，0.904，0.952}，基于相似度的修正系數{0.091，0.216，0.337，0.356}，修正后 3 號傳感器數據{0.080，0.123，0.770，0.027}，可以看出，與原始數據相比，修正后的數據更加精確。計算K’=0.4518，再將二者融合后的信任度與傳統 D-S 融合結果 0.875 相比，信任度提升到 0.933。
比較得出，基于數據修正的 D-S 證據理論多源數據融合診斷比傳統 D-S 證據理診斷效果好。
下面探究兩種方法的容錯能力，假如編號 3 傳感器發生故障，輸出歸一化的特征值為{0.20，0.42，0.26，0.12}，產生明顯異常，對應的狀態信任函數極低，甚至已經導致診斷的錯誤判斷，但編號 1、2 傳感器仍處于工作狀態，經過兩種方法多源數據融合，診斷結果比較如表 7 所示。
表7：傳感器 3 故障，融合前后診斷結果比較
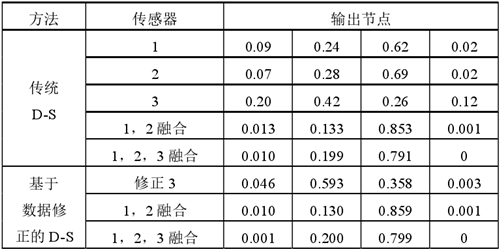
由表 7 結果，可以看出當一個傳感器發生故障時，傳統 D-S 證據理論的故障診斷信任度從 0.853 降低到0.791，診斷結果仍保持準確，而基于數據修正的 D-S證據理論故障診斷信任度從 0.859 降低到 0.799。比較得出，兩種方法均具備容錯能力，與單一傳感器相比，診斷效果好，且本文方法優于傳統 D-S 證據理論數據融合方法。
6、結束語
診斷結果比較表明，基于 Elman 網絡及數據修正D-S 證據理論的多源數據融合優于傳統 BP、RBF 及D-S 證據理論的融合方法，克服了單一傳感器故障導致的錯誤判斷，具有更高效、更快速的故障診斷能力，改善了單個傳感器診斷的不足，使診斷具備容錯能力， 大大提高了 D-S 證據理論的診斷準確性。
投稿箱：
如果您有機床行業、企業相關新聞稿件發表，或進行資訊合作，歡迎聯系本網編輯部， 郵箱：skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表，或進行資訊合作，歡迎聯系本網編輯部， 郵箱：skjcsc@vip.sina.com
更多相關信息
