摘要: 從自動化車床連續(xù)加工某種零件的故障檢測問題出發(fā)，探究了檢測方法與刀具更新對于生產(chǎn)附加成本的關(guān)系。建立了有更新點(diǎn)的檢查維護(hù)和預(yù)防性刀具更新的檢測優(yōu)化模型; 給出了自動化車床刀具檢測優(yōu)化模型研究檢查成本、不合格零件損失期望和包含故障維護(hù)費(fèi)用與刀具定期更換費(fèi)用的總維護(hù)費(fèi)用的期望的計(jì)算方法; 得到了以一定檢測間隔、預(yù)防性刀具更換周期為自變量的平均生產(chǎn)附加成本函數(shù)，取得了較優(yōu)定期檢測間隔和定期刀具更換間隔; 運(yùn)用蒙特卡洛隨機(jī)仿真的方法，進(jìn)行了仿真模擬，檢驗(yàn)了模型結(jié)果的優(yōu)越性。
 
     關(guān)鍵詞: 刀具; 更換策略; 檢測間隔; 條件概率; 蒙特卡洛模擬

      0 引言
 
     可靠性及維修性策略問題一直受到人們的廣泛關(guān)注和研究，通過設(shè)計(jì)系統(tǒng)可靠性及維修性策略，可提高重要產(chǎn)品和復(fù)雜工業(yè)系統(tǒng)的可靠性和可用性，降低生產(chǎn)成本。自動化車床管理是一個(gè)比較復(fù)雜的研究課題之一，要保持工序的正常運(yùn)行，需要經(jīng)常對工序進(jìn)行檢查。檢查周期長，可以減少檢查費(fèi)用，但由于不能及時(shí)發(fā)現(xiàn)故障會給生產(chǎn)帶來損失; 檢查周期短，雖然能夠及時(shí)發(fā)現(xiàn)故障少出不合格品，但檢查費(fèi)用高，因此，須找出最佳的檢查周期使得工序運(yùn)行單位時(shí)間內(nèi)的平均損失達(dá)到最小。
 
     由于自動化車床運(yùn)行中產(chǎn)生次品的故障主要為刀具故障，其它故障為小概率事件［1-2］，所以，在只考慮刀具故障的前提下，通過概率論和更新過程理論，建立以單位時(shí)間內(nèi)期望費(fèi)用為目標(biāo)函數(shù)的數(shù)學(xué)模型，以檢測間隔和刀具更換時(shí)刻為策略，確定最優(yōu)的策略使得工序長期運(yùn)行單位時(shí)間內(nèi)期望費(fèi)用達(dá)到最小。我們通過模型化的方法及一定的數(shù)學(xué)手段來求出較優(yōu)定期檢測間隔和定期刀具更換間隔，并尋求是否有更好的檢測策略。
 
      1 、問題的基本假設(shè)
 
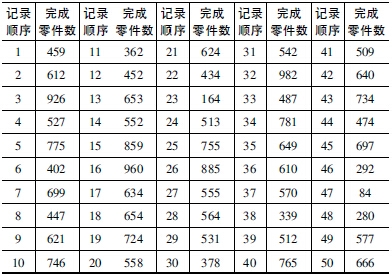
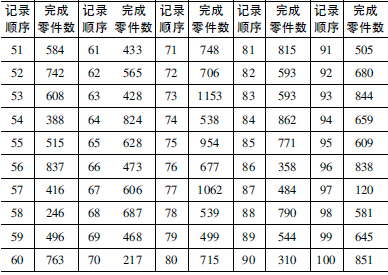
     用自動化車床連續(xù)加工某種零件，刀具損壞是出現(xiàn)故障的主要原因。現(xiàn)記錄了100 次故障出現(xiàn)時(shí)刀具完成的零件數(shù)，如表1 所示。
 
     問題1: 假設(shè)故障時(shí)產(chǎn)出均為不合格的零件，正常時(shí)產(chǎn)出均為合格的零件，設(shè)計(jì)效益最好的檢查間隔( 生產(chǎn)多少零件檢查一次) 和刀具更換策略。問題2: 如果正常時(shí)產(chǎn)出不全是合格的零件，有2%的不合格率; 而故障時(shí)產(chǎn)出的零件有40% 為合格率， 60%為不合格率。設(shè)計(jì)效益最好的檢查間隔和刀具更換策略。
 
     問題的基本假設(shè)如下:
 
     ( 1) 假設(shè)生產(chǎn)每個(gè)零件時(shí)工序出現(xiàn)故障是完全隨機(jī)的，且故障完全隨機(jī)。
     ( 2) 假設(shè)生產(chǎn)每個(gè)零件時(shí)刀具故障僅與刀具壽命有關(guān)。
     ( 3) 假設(shè)僅能通過檢測零件來判斷是否出現(xiàn)故障，即故障必須在檢查點(diǎn)才能被發(fā)現(xiàn)，且無法單純從一次檢驗(yàn)判斷該故障是刀具損壞故障還是其他故障。
     ( 4) 假設(shè)檢測零件過程不會出錯(cuò)，即對零件本身的不合格檢測沒有誤判。
     ( 5) 假設(shè)無論是95% 的刀具損壞故障還是5% 的其他故障，發(fā)生故障并使其恢復(fù)正常的平均費(fèi)用均為3000 元/次( 包括刀具費(fèi)用) 。每次恢復(fù)正常的過程都
進(jìn)行刀具更新操作。
     ( 6) 假設(shè)問題2 中工序正常時(shí)誤判為有故障停機(jī)產(chǎn)生的費(fèi)用( 1500 /次) 已包含刀具更換費(fèi)用，即刀具在誤判時(shí)被更新。零件時(shí)才進(jìn)行調(diào)整，即檢查次數(shù)的增多不會有更多
誤工損失。
 
 
                        表1 100 次刀具故障記錄( 完成零件數(shù))

     2 、問題分析
   
     自動化車床連續(xù)加工零件過程中會產(chǎn)生故障，故障后會導(dǎo)致不合格零件產(chǎn)生。通過定期檢測零件來檢測故障與維修，通過定期更換刀具預(yù)防工序故障。過長的檢查周期會導(dǎo)致故障不能及時(shí)被發(fā)現(xiàn)，大量不合格零件被生產(chǎn)，造成損失。過短的檢查周期又會造成檢查成本過高。類似的，過長的刀具更換周期無法起到很好的預(yù)防故障效果，過短的刀具更換周期又會使成本急劇上升。因此，兩個(gè)關(guān)鍵變量需要統(tǒng)籌兼顧，綜合考慮。
   
     此外，問題1 與問題2 需要分別進(jìn)行分析。問題1 假定工序故障是產(chǎn)出的零件均為不合格品，正常時(shí)產(chǎn)出的零件均為合格品。則通過零件合格與否來判斷工序故障為完全準(zhǔn)確。
 
     問題2 該工序正常時(shí)產(chǎn)出的零件不全是合格品，有2%為不合格品; 而工序故障時(shí)產(chǎn)出的零件有40%為合格品， 60% 為不合格品。則通過零件合格與否來判斷工序故障存在誤判風(fēng)險(xiǎn)，需要對誤判進(jìn)行條件概率的計(jì)算以準(zhǔn)確算出附加成本期望。
 
     綜上所述，該題要解決的是一個(gè)以單位附加成本最低為目標(biāo)，檢查間隔和換刀間隔為自變量的優(yōu)化問題［4-5］。

      3 、模型的建立
 
     3． 1 數(shù)據(jù)處理及故障間隔函數(shù)的確定
 
     根據(jù)給出的100 個(gè)刀具故障記錄，采用Matlab 軟件進(jìn)行數(shù)據(jù)處理，得到散點(diǎn)擬合圖，如圖1 所示。

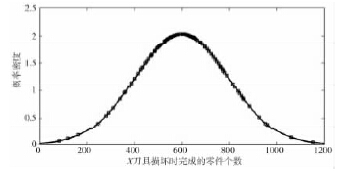
                          圖1 刀具故障記錄散點(diǎn)擬合圖
 
     由圖1 可知刀具壽命近似服從正態(tài)分布。可假設(shè)X 的概率密度函數(shù)為

     因此，在顯著性水平α = 0． 05 下接受總體服從正態(tài)分布。根據(jù)基本假設(shè)，非刀具故障，即其他故障在生產(chǎn)每個(gè)零件時(shí)的故障概率相同。因此，可得每個(gè)零件非刀具故障的概率p 為

     3． 2 基本模型的建立
 
     通過對問題的分析可知，該問題是一個(gè)單目標(biāo)優(yōu)化問題，其目標(biāo)函數(shù)為零件的平均附加成本F，F(xiàn) 的值越小則方案越優(yōu)。下面我們就零件平均成本的影響因素進(jìn)行分析，并建立相應(yīng)的基本數(shù)學(xué)模型。
 
     不難發(fā)現(xiàn)，整個(gè)生產(chǎn)附加成本由三部分組成，即檢查費(fèi)用，不合格零件損失費(fèi)用以及維護(hù)成本，其中維護(hù)成本又包含發(fā)現(xiàn)故障后的調(diào)整成本和定期換刀的預(yù)防成本。附加成本示意圖，如圖2 所示。

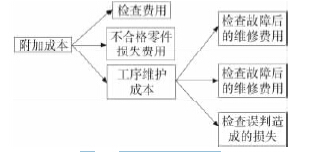
                            圖2 附加成本示意圖
  
     3． 2． 1 檢查過程
 
     由基本假設(shè)可知，檢查是通過對零件是否合格的檢查來判斷，設(shè)檢查過程是等間隔進(jìn)行的，間隔為N。顯而易見，檢查費(fèi)用= 檢驗(yàn)次數(shù)× 單次費(fèi)用，設(shè)共生產(chǎn)M 個(gè)零件，即有檢驗(yàn)費(fèi)用Et

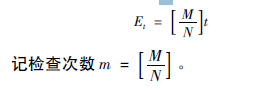
     左右兩個(gè)節(jié)點(diǎn)表示兩節(jié)點(diǎn)間整段生產(chǎn)過程情況。兩節(jié)點(diǎn)之間的區(qū)域稱之為一個(gè)區(qū)間。
   
      3． 2． 2 不合格零件損失費(fèi)用
   
     由于檢測方式是由零件是否合格來判斷，則若某檢查點(diǎn)發(fā)現(xiàn)零件不合格，則工序故障必定在兩個(gè)檢查點(diǎn)之間。但由于問題2 中存在著工序狀況與零件狀況不完全一致的概率，因而，問題1 和問題2 的不合格零件損失費(fèi)用需分別考慮。
 
     問題1: 工序故障時(shí)產(chǎn)出的零件均為不合格品，正常時(shí)產(chǎn)出的零件均為合格品。則若第k 次檢查出現(xiàn)了不合格品，那么工序故障必定發(fā)生在第( k － 1) 次檢查和第k 次檢查之間，即第( k － 1) n 個(gè)零件和第kn 個(gè)零件之間，如圖3 所示。

      
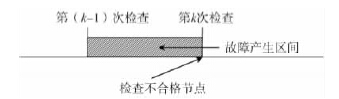
                        圖3 產(chǎn)生故障情況示意圖
   
     將這兩個(gè)檢查點(diǎn)之間的區(qū)間放大，可知共有n 個(gè)點(diǎn)可能發(fā)生工序故障。可以求得不合格零件損失費(fèi)用Ef。

     問題2: 如果該工序正常生產(chǎn)零件不全是合格品，有2%為不合格品; 工序故障時(shí)產(chǎn)出零件有40% 的合格品。因此，當(dāng)?shù)趉 次檢查檢查到不合格時(shí)，除去工序正常的誤判，工序故障的產(chǎn)生區(qū)間可能有不同的情況，除問題1 所示情況外，可能發(fā)生如圖4 所示的情況。

       
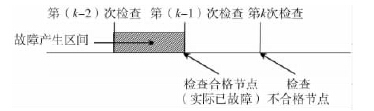
                             圖4 可能產(chǎn)生故障情況
   
     因此，不合格零件損失費(fèi)用期望的計(jì)算需要進(jìn)行改進(jìn)，即

      不合格零件由工序故障下產(chǎn)生次品和工序正常下產(chǎn)生次品兩部分構(gòu)成。其中工序故障下產(chǎn)生次品的概率不再是通過問題1 中簡單的工序故障區(qū)間進(jìn)行計(jì)算，故障產(chǎn)生區(qū)間存在條件概率［6-9］。‘
 
     工序故障記為FG，工序正常記為SG，檢查到次品FP，檢查到合格品SP。
 
     據(jù)貝葉斯公式，有

     3． 2． 3 維護(hù)成本
   
     維護(hù)成本是整個(gè)附加成本計(jì)算中的重要一環(huán)。維護(hù)成本包括兩個(gè)方面，分別為發(fā)生故障時(shí)調(diào)整設(shè)備產(chǎn)生的費(fèi)用及預(yù)防性更換刀具所產(chǎn)生的費(fèi)用。在問題2中，由于認(rèn)定工序故障存在誤判，所以維護(hù)成本中還需加入工序正常而誤認(rèn)為有故障停機(jī)的損失。
 
     基于以上討論，維護(hù)費(fèi)用期望值

     
  
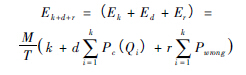
     其中Ek為預(yù)防性換刀的費(fèi)用期望，Ed為出故障調(diào)節(jié)的費(fèi)用期望，Er為誤判停機(jī)費(fèi)用期望( 對于問題一，Er = 0) 。該式中Pwrang為條件概率，由計(jì)算可知

     
  
     因此，節(jié)點(diǎn)換刀概率的遞推關(guān)系式為:
  
     
  
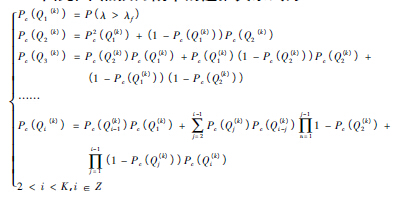
     其中P( λ ＞ λf) 是指此次( 換刀后第一次檢查行動) 判定為故障的概率。
 
     檢查過程的流程示意圖，如圖5 所示。

      
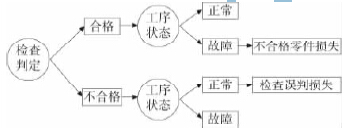
                           圖5 檢查過程的流程示意圖
   

      4 、結(jié)果分析
 
      4． 1 模型結(jié)果
 
     通過用Matlab 軟件對以上算法進(jìn)行計(jì)算機(jī)的算法實(shí)現(xiàn)，得到了問題1 的結(jié)果，如圖6 所示，檢查間隔18，檢查次數(shù)19，即預(yù)防性換刀周期為342，附加成本4． 890; 問題2 的結(jié)果，如圖7 所示，檢查間隔36，檢查次數(shù)13，即預(yù)防性換刀周期為468，附加成本9． 536。

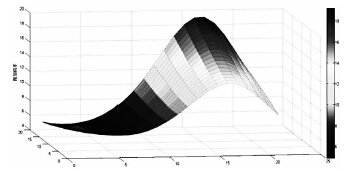
                               圖6 問題1 計(jì)算結(jié)果
   
  

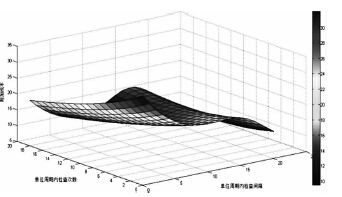
                           圖7 問題2 計(jì)算結(jié)果

      從這兩個(gè)結(jié)果發(fā)現(xiàn)，雖然問題2 中的檢查間隔變長，即檢查次數(shù)變少，但由于誤判的產(chǎn)生，多出了誤判成本，因而，單位附加成本顯著高于問題1 中的單位附加成本。
 
      4． 2 仿真模擬
   
     為了檢測算法的可行性，使用蒙特卡洛方法對問題一的算法進(jìn)行仿真模擬［10-11］，過程如下:
   
      ( 1) 給定換刀間隔T，檢查間隔N，以及生產(chǎn)零件個(gè)數(shù)M;
      ( 2) 設(shè)置連續(xù)不換刀生產(chǎn)的零件數(shù)S，已生產(chǎn)的零件個(gè)數(shù)F，生產(chǎn)損失和維護(hù)Y;
      ( 3) 從第一個(gè)零件開始，產(chǎn)生一個(gè)隨機(jī)數(shù)，檢測是否滿足先前擬合出來的概率，如果滿足，則將其之后一直到下一個(gè)檢查點(diǎn)的零件( 包括檢查點(diǎn)) 全部記為次品，并計(jì)算損失，計(jì)入Y; 如果不滿足，則進(jìn)入下一個(gè)零件的生產(chǎn)。
      ( 4) 對于第K 個(gè)零件，產(chǎn)生隨機(jī)數(shù)，檢測是否滿足之前擬合出來的概率，如果滿足，就將第K 個(gè)到K 之后距離最近的檢查點(diǎn)之間的所有零件( 包括檢查點(diǎn))記為次品，計(jì)算次品損失計(jì)入Y，然后在該檢查點(diǎn)處更換刀，將換刀損失計(jì)入Y; 如果不滿足，計(jì)入下一個(gè)零件生產(chǎn)，并令連續(xù)不換刀生產(chǎn)的零件數(shù)S = S + 1。將生產(chǎn)零件個(gè)數(shù)計(jì)入F;
      ( 5) 在檢查點(diǎn)處，如果發(fā)現(xiàn)連續(xù)不換刀生產(chǎn)的零件數(shù)S 大于T，則直接不檢查，然后換刀，將換刀成本計(jì)入Y;
      ( 6) F 大于M 時(shí)，停止生產(chǎn)，輸出對應(yīng)的T，N 所產(chǎn)生的費(fèi)用Y;
      ( 7) 取其它的T，N 值，進(jìn)行同樣的過程。對所有的Y 值進(jìn)行比較。

      取預(yù)防性換刀周期與檢查間隔為: ( 350，14 ) ，( 342， 18) ，( 396， 22) ，( 416，26) ，( 342，18) ，( 396，22)仿真模擬對比結(jié)果，如圖8 所示。

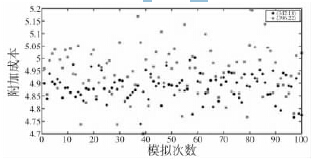
                               圖8 仿真模擬結(jié)果
     
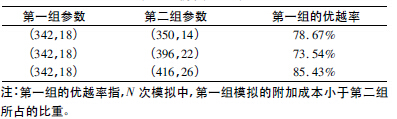
     由圖8 可知，在給定的較優(yōu)間隔處，附加成本在較低成本4． 95 附近，符合之前所設(shè)的概率規(guī)律。并且得到表2 所示的仿真對比表。仿真模擬的結(jié)果證明了算法是具有可行性。
 
 
                                         表2 仿真對比表

        
  
  
      5 、結(jié)論
   
      本文依據(jù)概率統(tǒng)計(jì)知識，建立了有更新點(diǎn)的檢查維護(hù)和預(yù)防性刀具更新的初等概率模型，給出了檢查成本、不合格零件損失期望和包含故障維護(hù)費(fèi)用與刀具定期更換費(fèi)用的總維護(hù)費(fèi)用的期望的計(jì)算方法，得到了以一定檢測間隔、預(yù)防性刀具更換周期為自變量的平均生產(chǎn)附加成本函數(shù)。運(yùn)用Matlab 計(jì)算，得到最優(yōu)解。運(yùn)用蒙特卡洛隨機(jī)仿真的方法，進(jìn)行了仿真模擬，檢驗(yàn)了模型結(jié)果的優(yōu)越性。